1

Querying and Maintaining a Compact XML Storage

Raymond K. Wong Franky Lam William M. Shui
National ICT Australia,
{raymond.wong, franky.lam, bill.shui}@nicta.com.au

Abstract:

As XML database sizes grow, the amount of space used for storing the data and auxiliary data structures becomes a major factor in query and update performance. This paper presents a new storage scheme for XML data that supports all navigational operations in near constant time. In addition to supporting efficient queries, the space requirement of the proposed scheme is within a constant factor of the information theoretic minimum, while insertions and deletions can be performed in near constant time as well. As a result, the proposed structure features a small memory footprint that increases cache locality, whilst still supporting standard APIs, such as DOM, and necessary database operations, such as queries and updates, efficiently. Analysis and experiments show that the proposed structure is space and time efficient.

H.3.2Information SystemsInformation Storage H.2.4.nTextual DatabasesXML Databases Algorithms, Design, Performance

1 Introduction

The popularity of XML as a data representation language has produced a wealth of research on efficiently storing and querying tree structured data. As the amount of XML data available increases, it is becoming vital to be able to not only query and maintain this information quickly, but also store it in a compact manner. Our work is also motivated by the mobile software development at National ICT Australia and Green Pea Software, in which managing large amount of XML data on mobile devices is mandatory. We thus turn to the problem of finding a compact storage scheme for XML, i.e., a space-efficient representation of the data structure which also maintains low access and update costs for all of the desired primitive operations for data processing. The flexibility of XML makes finding a scheme which satisfies all these requirements at the same time extremely challenging.

When looking for a compact storage scheme for XML, there are several issues that need to be addressed. For example, it has to support fast operations, especially we are considering software applications that target people on the move. Moreover, if intensive compression methods are employed, they need to be optional and can be switched on or off due to low computation power of some mobile devices. In summary, from our experience, the major issues include:

• It must support fast navigational operations: Many XML applications, such as collaborative document editing systems, depend upon efficient tree traversal, using a standard interface such as DOM. Halverson et al [10] demonstrated that a combination of navigational and structural join operators is most effective for evaluating queries. Hence, it is imperative that the storage scheme supports fast traversal of the XML tree, in all possible directions, preferably in constant time or near constant time. Previous work, such as that of Zhang et al [23], has addressed the issue of succinctly representing XML, but at the cost of linear time navigational operations, which is not acceptable for many practical applications. Our proposed structure efficiently supports tree navigation primitives in $O(\lg n / \lg \lg n)$ time, and also includes support for efficient structural joins.
• It must support efficient insertions and deletions: Several papers address the space issue by storing XML in compressed form [4,22,19,16]. They also support path expression queries or fast navigational access but do not allow efficient update operations such as node insertion. This can be a critical concern in many database applications. In this paper, we provide a scheme which allows near constant time for update operations in practice, with a theoretical worst case time of $O(\lg^2 n)$ .
• It must support efficient join operations: Current query optimization techniques for XML such as work of Halverson et al [10], make heavy use of the structural join [2], which relies on a constant time operator to determine the ancestor-descendant relationship between two nodes. Thus, any general XML storage scheme should also support such an operator in near constant time. Our scheme supports ancestor-descendant queries in $O(\lg n / \lg \lg n)$ time.
• It must be practical: Many succinct tree representation schemes are elegant theoretical structures that unfortunately do not translate well into practice. Thus, while theoretical guarantees are important for any proposed structure, practical considerations should not be forgotten. In this paper, we focus on developing a practical storage scheme, using values that fit to the natural machine word size, block size and byte alignment, to allow our scheme to be used in real-world database systems.
• It should separate the topology, schema and text of the document: All XML query languages select and filter results based on some combination of the topology, schema and text data of the document. To allow efficient scans over these parts of the document, it is natural to find a representation that partitions them into separate physical locations.
• It should permit extra indexes: Many applications may require addition specialized indexes to be built upon their data. Therefore, a general purpose database system is required to provide a storage representation, such that it is flexible enough to accommodate such need. More specifically, the storage scheme used by the database system must provide a simple, efficient and stable way of referencing its stored data items.

In this paper, we propose a compact XML storage engine, called ISX (for Integrated Succinct XML system), to store XML in a more concise structure and address all of the above issues. Theoretically, ISX uses an amount of space near the information theoretic minimum on random trees. For a constant $\epsilon$ , where $1 \le \epsilon \le 2$ , and a document with $n$ nodes, we need $2 \epsilon n + O(n)$ bits to represent the topology of the XML document. Node insertions can be handled in constant time on average but worst case $O(\lg^2 n)$ time, and all node navigation operations take worst case $O(\frac{\lg n}{\lg \lg n})$ time but constant time on average.

The rest of this paper is organized as follows: Section 2 summarizes relevant work in the field. Section 3 presents the basics of ISX and its topology layer. The fast node navigation operators, the querying interfaces and the update mechanism are then described in detail in Section 4. Finally, Section 5 presents the experiment results and Section 6 concludes the paper.

2 Related Work

To our best knowledge, Liefke and Suciu [16] proposed the first compressed XML scheme called XMill. Although XMill achieves a good compression ratio, its major drawback (which is the lack of support for query and update) hinders its broad application in database systems. Various approaches were proposed after XMill and they share similar benefits and drawbacks, e.g., XMLPPM [7].

Related work that share the same motivations with this paper includes Maneth et al [17], Tolani and Haritsa [22], Min et al [19] and Buneman et al [4]. Compared to XMill, XGrind [22] has a lower compression ratio but supports certain types of queries. XPRESS [19] uses reverse arithmetic encoding to encode tags using start/end regions. Both XGrind and XPRESS require top-down query evaluation, and do not support set-based query evaluation such as structural joins.

Buneman et al [4] separate the tree structure and its data. They then use bi-simulation to compress the documents that share the same sub-tree, however, they can only support node navigations in linear time. With a similar idea but different technique, Maneth et al [17,5] also compress XML by calculating the minimal sharing graph equivalent to the minimal regular tree grammar. In order to provide tree navigations, a DOM proxy that maintains runtime traversal information is needed [5]. Since only the compression efficiency was reported in the paper, both query and navigation performance of their proposed scheme are unclear.

Most XML storage schemes, such as [15,9,10,12], make use of interval and preorder/postorder labeling schemes to support constant time order lookup, but fail to address the issue of maintenance of these labels during updates. Recently, Silberstein et al [21] proposed a data structure to handle ordered XML which guarantees both update and lookup costs. Similarly, the L-Tree labeling scheme proposed by Chen et al [6] addressed the same problem and has the same time and space complexity as [21], however, they do not support persistent identifiers. The major difference between our proposal and these two work is that we try to minimize space usage while allowing efficient access, query and update of the database. In this paper, we show that our proposed topology representation costs linear space while [21] costs $n\: log\: n$ space.

The work most related to this paper regarding databases with efficient storage is from Zhang et al [23]. The succinct approach proposed by Zhang et al [23] targeted secondary storage, and used a balanced parentheses encoding for each block of data. Unfortunately, their summary and partition schemes support rank and select operations in linear time only. Their approach also uses the Dewey encoding for node identifiers in their indexes. The drawbacks of the Dewey encoding are significant: updates to the labels require linear time, and the size of the labels is also linear to the size of the database in the worst case. Thus, the storage of the topology can require quadratic space in the worst case.

Finally, there are several related proposals published recently, e.g. [9,8]. [9] show that all XPath axes can be handled using a preorder/postorder labeling. Instead of maintaining these two labels (i.e., two integers), our proposed scheme requires less than 3 bits per node to process all XPath axes, which is an attractive alternative for applications that are both space and performance conscious.

Ferragina et. al.[8] first shred the XML tree into a table of two columns, then sort and compress the columns individually. It does not offer immediate capability of navigating or searching XML data unless an extra index is built. However, the extra index will degrade the overall storage size (i.e., the compression ratio). Furthermore, the times for disk access and decompression of local regional blocks have been omitted from their experiments. As a result, the performance of actual applications may be different from what the experiments shown. Same as most other related work, data updates have been disregarded.

3 ISX Storage and Topology
Layer

Figure 1: A DBLP XML document fragment

This section describes the storage layer of the ISX system. It consists of three layers, namely, topology layer, internal node layer, and leaf node layer. In Figure 3, the topology layer stores the tree structure of the XML document, and facilitates fast navigational accesses, structural joins and updates. The internal node layer stores the XML elements, attributes, and signatures of the text data for fast text queries. Finally the leaf node layer stores the actual text data. Text data can be compressed by various common compression techniques and referenced by the topology layer.

Figure 2: Overview of the data structure

Figure 3: Balanced parentheses encoding of Figure 1

1 ISX Topology Layer

Jacobson [11] showed that the lower bound space requirement for representing a binary tree is $\lg(C_n) = \lg(4^n \cdot \Theta(n^{-\frac{3}{2}})) = 2n+o(n)$ bits, where the Catalan number $C_n$ is the number of possible binary trees over $n$ nodes.

Our storage scheme is based on the balanced parentheses encoding from [14], representing the topology of XML. Different from [14], our topology layer (Figure 3) actually supports efficient node navigation and updates.

The balanced parentheses encoding used in tier 0 reflects the nesting of element nodes within any XML document and can be obtained by a preorder traversal of the tree: we output an open parenthesis when we encounter an opening tag and a close parenthesis when we encounter a closing tag. In Figure 3, the topology of a DBLP XML fragment shown in Figure 1 is represented in tier 0 using the balanced parentheses encoding. In our implementation, we use a single bit 0 to represent an open parenthesis and a single bit 1 to represent a close parenthesis.

2 Representation of Elements, Attributes and Texts

We avoid any pointer based approach to link a parenthesis to its label, as it would increase the space usage from $2n$ to a less desirable $\Theta(n\lg n)$ . As our representation of the topology also does not include a $O(\lg n)$ bit persistent object identifier for each node in the document, we must find a way to link the open parenthesis of $x$ in tier 0 to the actual label itself. To address this, we adopt from Munro's work [20] although they do not use balanced parentheses encoding. Instead, they control the topology size by using multiple layers of variable-sized pointers, and may require many levels of indirection. In addition, we make the element structure an exact mirror of the topology structure instead of mirroring to the pointers. This allows us to find the appropriate label for a node by simply finding the entry in the corresponding position at the element structure. As mentioned earlier, a pointer based approach would require space usage of $\Theta(n\lg n)$ , which is undesirable. The next issue is to handle the variable length of XML element labels. We adopt the approach taken in previous work [22,23], and maintain a symbol table, using a hash table to map the labels into a domain of fixed size. In the worst case, this does not reduce the space usage, as every node can have its own unique label. In practice, however, XML documents tend to have a very small number of unique labels. Therefore, we can assume that the number of unique labels used in the internal nodes ($E$ ) is very small, and essentially constant. This approach allows us to have fixed size records in the internal node layer.

Note that each element in the XML document actually has two available entries in the array, corresponding to the opening and closing tags. We could thus make the size of each entry $\frac{1}{2}\lg E$ bits, and split the identifier for each elements over its two entries. However, the two entries are not in general adjacent to each other, and hence splitting the identifier could slow down lookups as we would need to find the closing tag corresponding to the opening tag and decrease cache locality. Hence, we prefer to use entries of $\lg E$ bits and leave the second entry set to zero; this also provides us with some slack in the event that new element labels are used in updates.

Since text nodes are also leaf nodes, they are represented as pairs of adjacent unused spaces in the internal node layer. We thus choose to make use of this ``wasted'' space by storing a hash value of the text node of size $2\lg E$ bits. This can be used in queries which make use of equality of text nodes such as /$$ /*[year="2003"], by scanning the hash value before scanning the actual data to significantly reduce the lookup time. Since texts are treated independently from the topology and node layers, they can be optionally compressed by any compression schemes. Instead of employing more sophisticated compression techniques such as BWT [8] that are relatively slow on mobile devices, a standard LZW compression method (e.g., gzip) is used in this paper.

4 Querying and Update
Maintenance

In addition to efficiently storing large volumes of data, an XML database system should also have the following features: 1) direct node navigation operators; 2) XPath query processing interface; and 3) efficient node insertion/deletion mechanism. For the rest of this section, we present algorithms and other auxiliary data structures satisfying the above features, utilising the ISX topology layer. Furthermore, we provide a detailed cost analysis of our proposed approach for the database operators.

1 Node Navigation with Topology Layer Primitives

Given an arbitrary node $x$ of a large XML document, a navigation operator should be able to traverse back and forth the entire document via various step axes of node $x$ . Some frequently used step axes for an XML document tree are parent, first-child, next-sibling, previous-sibling, next-following and next-preceding. These step axes can then be used to provide programming interfaces, such as the DOM API, for external access to the XML database.

Node navigation operators are described by the pseudo-code in Algorithm 1, which shows a tight coupling between the ISX topology layer primitives and the navigation operators. Each navigation operator in Algorithm 1 is mapped to a sequence of calls to the topology layer primitives described in Algorithm 2.

2 Auxiliary Tiers

Figure 4: Example of Tiers of Topology Part

Node navigation operators are highly dependent on topology layer primitives such as FORWARDEXCESS and BACKWARDEXCESS. In the worst case, node navigation operators could take linear time. However, we can significantly improve the performance of the topology layer primitives by adding auxiliary data structures (tier 1 and tier 2 blocks) on top of the tier 0 layer described in Section 3.1.

Figure 4 presents the auxiliary tiers 1 ($T^1$ ) and 2 ($T^2$ ), where each tier contains contiguous arrays of tuples, with each tuple holding summary information of one block in the lower tier. The tier 0 in the figure corresponds to the balanced parentheses encoding of the topology of the XML document, which was described in Section 3. For tiers 1 and 2, each tier 1 block stores an array of tier 0 tuples $T^0_1, T^0_2, \dots , T^0_n$ , where $n$ is the maximum number of tuples allowed per tier 1 block. Each $T^0_i$ for $0 < i \leq n$ is defined as $(L^0, R^0, m^0, M^0, b^0, B^0, D^0)$ and the density of each tier 0 block can be calculated by using the formula $density = \frac{L^0 + R^0}{\vert\B\vert}$ . For each tier 0 tuple, $L^0$ is the total number of left parentheses of a block; $R^0$ is the total number of right parentheses of a block; $m^0$ is the minimum excess within a single block by traversing the parentheses array forward from the beginning of the block; $M^0$ is the maximum excess within a single block by traversing the parentheses array forward from the beginning of the block; $b^0$ is the minimum excess within a single block by traversing the parentheses array backward from the last parenthesis of the block; $B^0$ is the maximum excess within a single block by traversing the parentheses array backward from the last parenthesis of the block; and $D^0$ is total number of character data nodes. In tier 2, each block stores an array of tier 1 tuples $T^1_1, T^1_2, \dots, T^1_n$ , where $n$ is the maximum number of tuples allowed per tier 2 block, Each tuple $T^1_i$ for $0 < i \leq n$ is then defined as $(L^1, R^1, m^1, M^1, b^1, B^1, D^1)$ , where: $L^1$ is the sum of all $L^0$ for all tier 1 tuples $T^0$ ( $\sum^{\vert\B\vert/\vert T^0\vert}_{i=0}{L^0_i}$ ); $R^1$ is the sum of all $R^0$ for all tier 1 tuples $T^0$ ( $\sum^{\vert\B\vert/\vert T^0\vert}_{i=0}{R^0_i}$ ); $m^1$ is the local forward minimum excess across all of its tier 1 tuples; $M^1$ is the local forward maximum excess across all of its tier 1 tuples; $b^1$ is the local backward minimum excess across all of its tier 1 tuples; $B^1$ is the local backward maximum excess across all of its tier 1 tuples; and $D^1$ is the total number of character data nodes for all tier 1 tuples ( $\sum^{\vert\B\vert/\vert T^0\vert}_{i=0}{D^0_i}$ ).

Although both tier 1 and tier 2 tuples look similar, the values of $m^1$ , $M^1$ , $b^1$ and $B^1$ in tier 2 are calculated differently to that of in tier 1. For tier 2, the function TIER2LOCALEXCESS in Algorithm 3 is used to calculate the local minimum/maximum excess and it is not as trivial as the calculation for tier 1 blocks.

Let $X = (L,R,m,M,b,B,D)$ be a tier 2 tuple holding the summary information for the tier 1 tuples ${Y1, \dots, Yn}$ . To calculate the local forward minimum excess $X.m$ , we know the local minimum excess from the beginning of the first parentheses of $Y1$ until the end of $Y1$ is equal to $Y1.m$ , we then assign this value to $X.m$ . We know the excess at the end of $Y1$ is $Y1.L-Y1.R$ , so the minimum of $Y1.m$ and $(Y1.L-Y1.R+Y2.m)$ gives the forward minimum excess from beginning parenthesis of $Y1$ to the end parenthesis of $Y2$ . Similarly, the minimum of $(Y1.m,Y1.L-Y1.R+Y2.m, Y1.L-Y1.R+Y2.L-Y2.R+Y3.m)$ gives the minimum excess between the beginning parenthesis of $Y1$ to the end parenthesis of $Y3$ . Therefore, $X.m$ can be calculated by scanning its tier 1 tuples, updating the excess along the way. Both maximum and minimum forward excesses can be calculated at the same time. For backward excesses, the algorithm is identical, except for the direction of traversal of the tier 1 tuples.

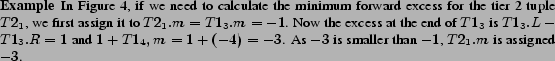
In the ISX system, the fixed block size for each tier is 4 kilobytes in size. Therefore, each tier 0 block can hold up to 32768 bits and each tier 1 block can hold $\frac{4{\rm KB}}{\vert T^0\vert}$ tier 0 blocks. Similarly, each tier 2 block can hold up to $\frac{4{\rm KB}}{\vert T^0\vert}$ tier 1 blocks, which is equivalent to $(\frac{4{\rm KB}}{\vert T^0\vert})^2$ tier 0 blocks. For a 32-bit word machine, there are only 2 tier 2 blocks and in theory, there are $\Theta(n / \lg^2 n)$ tier 2 blocks. Therefore, the worst case for navigational accesses is $O(n / \lg^2 n)$ , which is not much of an improvement on $O(n)$ . Fortunately, it is relatively simple to fix this limitation: instead of having $3$ tiers, we generalize the above structure in a straightforward fashion to use $O(\lg n / \lg \lg n)$ tiers. This means that the top-most tier has $\Theta(n / \lg^{\lg n / \lg \lg n} n) = \Theta(1)$ blocks, reducing the worst case navigational access time to $O(\lg n / \lg \lg n)$ .

3 Improved Topology Layer Primitives

FORWARDEXCESS and BACKWARDEXCESS return the position of the first parenthesis matching the given excess $k$ within a given range $[start,end]$ (in forward and backward direction respectively).

Using the auxiliary structures (tiers 1 and 2), instead of just a linear scan of tier 0 layer, we can use tier 1 to test whether the position of the parenthesis, matching $k$ excess, lies within the $i$ -th tier 0 block, i.e., checking whether $(m^0_i + e_i) \leq k \leq (M^0_i + e_i)$ , where $e_i$ is the excess between $start$ and the beginning of the $i$ -th tier 0 block (excluding the first bit). However, as $\vert\B\vert=\Theta(\lg n)$ , there are potentially $n/\vert\B\vert$ tier 1 tuples to scan. Hence, we use tier 2 find the appropriate tier 1 block within which $excess$ lies, thus reducing the cost to a near constant in practice.

Using the above approach, we can replace primitives NEXT, FORWARDEXCESS and BACKWARDEXCESS in Algorithm 2 with improved primitives in Algorithm 4. Furthermore, since the depths of real-world XML documents are generally less than $\vert\B\vert$ (even the depth of the highly nested Tree Bank dataset [18] is much less than 100), most matching parentheses lie within the same block, and occasionally are found in neighboring blocks. Therefore, when FASTFORWARDEXCESS is called from navigation operations, we rarely need to access additional blocks in either the auxiliary data structure or the topology bit array. In the worst case, when the matching parentheses lie within different blocks, we only need to read two tier 1 blocks and two tier 2 blocks for a 32-bit word size machine, which is very small in size.

4 Update Operators

In ISX system, we also facilitate efficient update operators, such as node insertion. So far for tier 0 layer, we have appeared to treat the balanced parentheses encoding as a contiguous array. This scheme is not suitable for frequent updates as any insertion or deletion of data would require shifting of the entire bit array.

1 Updating Tier 0

In this section, we present the modification to our storage scheme, that changes the space usage from $2n$ to $2\epsilon n$ , where $\epsilon\ge 1$ , so that we can efficiently accommodate frequent updates.

Figure: Densities of the parentheses array and the corresponding virtual balanced trie with block size $\vert\B\vert = 8$ and ${\rm height} = 3$ .

In our approach, we first divide the array into blocks of $\vert\B\vert$ bits each, and store the blocks contiguously. Within each block, we leave some empty space by storing them at the rightmost portion of each block. Now, we only need to shift $O(\vert\B\vert)$ entries per insertion or deletion. We can control the cost of shifting by adjusting the block size.

After the initial loading of an XML document, the empty space allocated to leaf nodes will eventually be used up as more data is inserted into the database. Therefore, we need to guarantee an even distribution of empty bits across the entire parentheses array, so that we can still maintain the $O(\vert\B\vert)$ bound for the number of shifts needed for each data insertion. This can be achieved by deciding exactly when to redistribute empty space among the blocks and which blocks are to be involved in the redistribution process.

To better understand our approach, we first visualize these blocks as leaf nodes of a virtual balanced binary trie, with the position of the block in the array corresponding to the path to that block through the virtual binary trie. Figure 5 shows such a trie, where block 0 corresponds to the leaf node under the path $0\!\to\!0\!\to\!0$ , and similarly block 3 corresponds to the path $0\!\to\!1\!\to\!1$ . For each block, we define:

• $L$ : the total number of left parentheses within a block.
• $R$ : the total number of right parentheses within a block.
• DENSITY($b$ ): the density of a block $b$ , defined as $\frac{L+R}{\vert\B\vert}$ .

Given the above definition of density for leaf nodes, the density of a virtual node is the average density of its descendant leaf nodes. We then control the empty space within all nodes in the virtual binary trie by setting a density threshold $[min, max]$ , within which the block densities must lie. For a virtual node at height $h$ and depth $d$ in the virtual trie, we enforce a density threshold of $[\frac{1}{2} - \frac{d}{4h}, \frac{3}{4} + \frac{d}{4h}]$ . For example, the density threshold range for virtual node $v_{0}$ in Figure 5 is $[\frac{1}{2}-\frac{2}{4\times3},\frac{3}{4}+\frac{2}{4\times3}] = [0.33, 0.92]$ , since the depth for $v_{0}$ is 2 and height of the trie is 3.

Why do we use the formula above for controlling the density threshold? This is due to two factors: first, in order to guarantee good space utilization, the maximum density of a leaf node should be 1, and the minimum density threshold of root node should be $1/2$ . Secondly, the density threshold should satisfy the following invariant: the density threshold range of an ancestor node should be tighter than the range for its descendant nodes. This is so that space redistribution for an ancestor node $v$ , the density threshold of all its descendants are also immediately satisfied.

In the worst case, we use $4$ bits per node, since the root node can be only half full. Thus, on a $32$ -bit word machine, we can store at most $2^{32}/4 = 2^{30}$ nodes. However, by adjusting the minimum root node density threshold, from $\frac{1}{2}$ to $\frac{1}{\epsilon}$ it is possible to store more than $2^{30}$ nodes by choosing a smaller $\epsilon$ . In practice, $\epsilon$ should be $2$ and therefore $2\epsilon{}n$ bits is in effect $4n$ . The factor $\epsilon$ should only be less than $2$ when the document is relatively static.

Notice that although we shift the parentheses within tier 0 during update, we never need to shift the tuples in tier 1 because the same $T^0$ tuple always corresponds to the same tier 0 block, regardless of its density. Therefore unlike tier 0, we do not need to redistribute tuples within tier 1 (similarly for tier 2) during the update operation.

2 Updating Auxiliary Tiers

From Section 4.2, the auxiliary tiers may first appear to increase the update costs to $O(\lg^3 n / \lg \lg n)$ , since moving a node requires updating $O(\lg n / \lg \lg n)$ tiers. However, this overhead can be eliminated by updating the upper tiers once per redistribution, instead of once per node. A simple proof then demonstrates that the overall update cost is unaffected, and remains $O(\lg^2 n)$ .

During the insertions and deletions in a tier 0 block, we simply update the appropriate tuples in the corresponding blocks in the higher tiers. Since the redistribution process we described in Section 4.4.1 can be seen as a sequence of insertions and deletions, the corresponding updates to the auxiliary tiers do not affect the worst case complexity for updates.

5 Space Cost

Having $2\epsilon{}n$ bits used per node including update, using 32-bits word, we can store as much as $2^{30}$ nodes. In our implementation we also chose to use four kilobytes sized block. Based on these values, we now discuss the space cost of each component of our storage scheme. Of course, if larger documents need to be stored, we can increase the word size that we use in the data structure and adjust the bit length used on tier 1 and tier 2.

Tier 0:

From above, Tier 0 can take up at most $2^{32/2\epsilon} = 2^{32}$ bits space (or $\lceil\frac{2\epsilon n}{\vert\B\vert}\rceil=2^{17}$ blocks).

Tier 1:

We need $\lg\vert\B\vert=15$ bits for each variable $(L^0, R^0, m^0, M^0, b^0, B^0, D^0)$ within a $T^0$ tuple. Each $T^0$ tuple requires a total of $7\lg\vert\B\vert=112$ bits including bit alignments and based on this calculation, each tier 1 block can then store up to $\lfloor\frac{\vert\B\vert}{\vert T^0\vert}\rfloor=292$ $T^0$ tuples, Since the maximum number of nodes can be stored in tier 0 is $2^{30}$ , then we only need $\frac{2\epsilon n}{\vert\B\vert}=2^{17}$ $T^0$ tuples to represent all tier 0 blocks and they can be stored in $\big\lceil\frac{2\epsilon n}{\vert\B\vert}/\lfloor\frac{\vert\B\vert}{\vert T^... ...\big\rceil = \lceil\frac{14\lg\vert\B\vert\epsilon n}{\vert\B\vert^2}\rceil=449$ tier 1 blocks.

Tier 2:

We need a total of 24 bits for each variable $(L^1, R^1, m^1, M^1, b^1, B^1, D^1)$ within a $T^1$ tuple. This is derived from $\lg\vert\B\vert+\lg(\frac{\vert\B\vert}{\vert T^0\vert})=\lg(\frac{\vert\B\vert^2}{7\lg\vert\B\vert})$ , where each variable holds the size of a tier 1 tuple and total number of bits required to represent the total number of tuples per tier 1 block. So each $T^1$ tuple requires a total of $\vert T^1\vert=7\lg(\frac{\vert\B\vert^2}{7\lg\vert\B\vert})=168$ bits and each tier 2 block holds up to $\lfloor\frac{\vert\B\vert}{\vert T^1\vert}\rfloor=195$ $T^1$ tuples. Thus, we will only need a total of $\lceil\frac{14\lg\vert B\vert\epsilon n}{\vert\B\vert^2}/\frac{\vert\B\vert}{\... 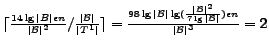...\vert\lg(\frac{\vert\B\vert^2}{7\lg\vert\B\vert})\epsilon{}n}{\vert\B\vert^3}=2$ tier 2 blocks to store the 449 tier 1 tuples.

Since we only need a maximum of two tier 2 blocks, even for $2^{30}$ nodes document, we can just keep them in main memory. In fact, the entire tier 1 can also be kept in main memory, since it requires at most $449*4\mathrm{KB}<2\mathrm{MB}$ . In summary, the space required by the topology layer (in bits) is:

$$2\epsilon{}n + \frac{14\lg\vert\B\vert\epsilon{}n}{\vert\B\vert} ... ...{7\lg\vert\B\vert})\epsilon{}n}{\vert\B\vert^2}= 2\epsilon{}n + o(\epsilon{}n)$$

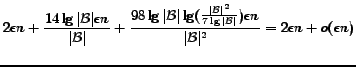
and the space required by the internal node layer (in bits) plus the symbol table is: $\epsilon n\lg E + O(E)$

We can use the above equations to estimate the space used by an XML file, using as our example a 100 MB copy of DBLP, which was roughly 5 million nodes. If we assume there are no updates after the initial loading, we can set $\epsilon{}=1$ . According to the equation, we will have used roughly $2\epsilon{}n = 1\mathrm{MB}$ for the topology layer, and $\epsilon{}n\lg E + O(E) = 8\mathrm{MB}$ . This, of course, disregards the space needed for the text data in the document.

Based on the block size $\vert\B\vert$ , we know the exact size of tuples and tiers in our topology layer. Therefore, given a bit position $x_\langle$ , we can calculate which tier 0 block this bit belongs to and which tier 1 block contains summary information for the tier 0 block. For a given $x_\langle$ , Algorithm 6 lists all the calculations needed to find its resident tier 0 to tier 2 blocks and the index within the blocks to get the summary.

5 Experiments

Table 1: Comparison of supported features

Features	XMill	XGrind	NoK	TIMBER	ISX
Compression	$\surd$	$\surd$			$\surd$
Doc traversal	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$
Node nav.of all axes			uncertain	$\surd$	$\surd$
Update operation				$\surd$	$\surd$
Support XPath query		$\surd$	$\surd$	$\surd$	$\surd$

The ISX system is implemented in C++ using Expat XML parser¹. In this section, we compare the performance of ISX with other related implementations, namely, XMill [16], XGrind [22], NoK [23] and TIMBER [12]. Experiments were setup to measure various performances according to the feature matrix of these implementations as shown in Table 1.

We used an Apple G5 2.0 GHz machine with 2.5GB RAM and 160GB of 7,200 RPM IDE hard drive. The memory buffer pool of ISX has been fixed to 64MB for all the experiments. Three XML datasets were used, namely, DBLP [1], Protein Sequence Database (PSD) [3], TreeBank [18]. We found that the experiment results from PSD are very similar to those from DBLP due to their regular, shallow tree structure. Therefore, PSD results are skipped from some plots below for clarity. Large datasets (i.e., $\geq$ 1GB) were generated by repeatedly duplicating and merging the source dataset, e.g., the 16GB DBLP document contains more than 770 million nodes.

1 Storage Size Comparison

Table 2: Storage size of ISX (with and without text compression), XMill and XGrind on DBLP

Source Data	ISX	ISX	XMill	XGrind	Source Data	ISX	ISX	XMill	XGrind
(MB)	(MB)	Compressed (MB)	(MB)	(MB)	(MB)	(MB)	Compressed (MB)	(MB)	(MB)
1	1	0.4	0.1	0.3	256	182	82.7	31.5	75.0
2	1	0.7	0.3	0.6	500	363	163.7	62.6	Failed
5	3	1.5	0.5	1.3	750	549	249.7	94.0	Failed
8	5	2.5	0.9	2.1	1000	726	327.5	125.3	Failed
16	10	5	1.8	4.3	2000	1452	654.9	250.5	Failed
32	21	10	3.7	8.6	4000	2903	1309.8	501.0	Failed
64	42	20	7.2	17.4	8000	5807	2619.6	978.48	Failed
128	87	40.2	14.9	35.8	16000	9411	4629.9	1952.81	Failed

Table 3: Storage size of ISX (with and without text compression), XMill on TreeBank

Source Data	ISX	ISX	XMill	Source Data	ISX	ISX	XMill
(MB)	(MB)	Compressed (MB)	(MB)	(MB)	(MB)	Compressed (MB)	(MB)
1	0.51	0.41	0.30	256	131.08	104.53	73.38
2	1.02	0.81	0.58	500	243.72	192.79	146.74
4	2.04	1.63	1.16	750	365.50	289.21	220.10
8	4.09	3.26	2.30	1000	487.43	385.58	293.489
16	8.19	6.53	4.60	2000	974.69	770.98	586.969
32	16.39	13.07	9.19	4000	1949.39	1541.97	1173.93
64	32.77	44.49	18.35	8000	4052.58	3205.59	2347.85
128	65.54	52.26	36.69	16000	7797.56	6167.87	4695.7

Table 2 and 3 show that XMill has the best compression ratio for both DBLP and TreeBank datasets. Compared to XMill that does not support any direct data navigation and queries, XGrind does allow simple path expressions. Therefore, it has a relatively less attractive compression ratio. In fact, XGrind failed to run on large datasets in our experiments. Both XMill and XGrind have better space consumption as they are primarily designed for read-only data and do not support efficient updates. Furthermore, they only support access to the compressed data in linear time.

Table 2 and 3 show again that ISX is relatively less sensitive to the structure of the data. Although the compression ratio of ISX for TreeBank is not as good as for DBLP, the reason is that TreeBank has the text content that are harder to compress (TreeBank text are more random than the DBLP's). XMill compression ratio on TreeBank is relatively much worse than that on DBLP is due to both the random text content as well as the more complex tree structure of the data.

2 Bulk Loading Performance

The performance comparison of bulk loading using ISX, NoK, XGrind and XMill are shown in Figure 6. For the smaller datasets (up to 500MB DBLP), Figure 6(a) shows our ISX system significantly outperforms NoK and TIMBER in loading. It also highlights the scalability of ISX in loading large datasets.

Figure 6: Loading Time Comparison

[ISX vs. TIMBER and NoK (up to 500 MB data)]

[ISX vs. XGrind and XMill (up to 16 GB data)]

To further test the scalability of loading even larger XML documents, we compared the loading time of ISX and the other well known systems such as XMill and XGrind on 1 to 16 GB of DBLP documents. During the loading process, XGrind failed to load XML documents greater than 100MB. Although Figure 6(b) shows that the loading time for ISX is slower than XMill's, it still exhibits a similar trend (similar scalability). The gap between the two curves is contributed by the fact that ISX does not compress the XML data as much as XMill does. This results in a larger storage layer than XMill, which will then uses higher number of disk writes.

3 Query Performance

Table 4: Test Queries and Final Result Sizes

Query $\char93$	XPath Expression	1 GB	2 GB	4 GB	8 GB	16 GB
		$\vert Final\vert$	$\vert Final\vert$	$\vert Final\vert$	$\vert Final\vert$	$\vert Final\vert$
Q1	$//inproceedings$	402667	981484	2012761	4160339	8453066
Q2	$//mastersthesis$	74	156	315	627	1251
Q3	$/dblp/article$	442184	717449	1379945	2630711	5135130
Q4	$//inproceedings/title$	402667	981484	2012761	4160339	8453066
Q5	$//article[.//month/text()=''July'']//title$	857309	1729184	3454708	6920136	13848372
Q6	$//inproceedings[.//ee]//pages$	796742	1607116	3210628	6430194	12868471

When consider using the proposed structure as a storage scheme of a full-fledged database system, one must consider its query performance. Figure 7 (with details listed in Tables 4) shows the query performance of ISX against other schemes. Note that the query times in Figure 7 are in logarithmic scale. From this experiment, we found that ISX outperforms other systems in either the ISX or ISX Stream (using the TurboXPath approach [13]) modes. The performance of ISX is measured by using binary structural join to perform XPath queries; while ISX Stream execute the same query by scanning ISX topology layer linearly.

Figure 7: Query Performance (in log scale) of ISX vs. Other Systems

[DBLP Q1]

[DBLP Q2]

[DBLP Q3]

[DBLP Q4]

[DBLP Q5]

[DBLP Q6]

4 Navigation and Document Traversal

Figure 8: Navigation and traversal performance time of ISX

[Node navigation time (microseconds)]

[Full document traversal time (seconds)]

To test the performance and scalability of random node navigation, we pre-loaded our XML datasets, and for each database, we randomly picked a node and called the node traversal functions (e.g., FIRSTCHILD, NEXTSIBLING) multiple times. The average access time for these node traversal operations are plotted in Figure 8(a). The graph shows that as the database size gets bigger, the running time for these functions remains constant. This is not surprising, since in general most nodes are located close to their siblings, and hence are likely to be in the same block. For example, it generally only takes a scan of a few bits on average to access either the first child node or the next sibling node. Some operations are faster than the others, due to their different implementation complexity (listed in Algorithm 1) and the characteristics of the encoding itself. For instance, as Figure 8(a) shows, FIRSTCHILD performed slightly faster than NEXTSIBLING function, because the first child is always adjacent to a node, whereas its next sibling might be several nodes away.

With fast traversal operations, ISX can traversal XML data in the proposed compact encoding significantly faster than other XML compression techniques such as XMill, as shown in Figure 8(b). We argue that this feature is important to examine the content of large XML databases or archives.

5 Update Performance

Figure 9: Insertion time of ISX using 128 MB - 16 GB DBLP

The worst case for Algorithm 5 happens when nodes are inserted at the beginning of a completely packed database, i.e., with no gaps between blocks. The insertion experiment was set to measure its average worst case performance by inserting nodes at the beginning of the database. For each experiment, we did multiple runs (resetting the database after each run). The average insertion times (per node) are shown in Figures 9. In Figure 9, we see an initial spike in the execution time for the worst case insertion. This corresponds to the initial packed state of the database, in which case the very first node insertion requires the redistribution of the entire leaf node layer. Clearly, in practice this is extremely unlikely to happen, but the remainder of the graph demonstrates that even this contrived situation has little effect on the overall performance. The graph also shows that the cost of all subsequent insertions increases at a rate of approximately $O(\lg^{2}n)$ . In fact, all subsequent insertions up to 100,000 took no more than 0.5 milliseconds.

Updating the values of nodes will not cause extra processing time apart from the retrieval time for locating the nodes to be updated. In case of deletion, the reverse sequence of steps for node insertion will be performed (freed space will be left as gaps to be filled by subsequent insertions).

6 Conclusions

A compact and efficient XML repository is critical for a wide range of applications such as mobile XML repositories running on devices with severe resource constraints. For a heavily loaded system, a compact storage scheme could be used as an index storage that can be manipulated entirely in memory and hence substantially improve the overall performance. In this paper, we proposed a scalable and yet efficient, compact storage scheme for XML data.

Our data structure is shown to be exceptionally concise, without sacrificing query and update performance. While having the benefits of small data footprint, experiments have shown that the proposed structure still out-performs other XML database systems and scales significantly better for large datasets. In particular, all navigational primitives can run in near constant time. Furthermore, as shown in the experiments, our proposed structure allows direct document traversal and queries that are significantly faster and more scalable than previous compression techniques.

Bibliography

1

Dblp bibliography.
See http://www.informatik.uni-trier.de/~ley/db/.

2

Shurug Al-Khalifa, H. V. Jagadish, Nick Koudas, and Jignesh M. Patel.
Structural joins: A primitive for efficient XML query pattern matching.
In Proceedings of the 18th International Conference on Data Engineering (ICDE), pages 141-153. IEEE Computer Society, 2002.

3

Rolf Apweiler, Amos Bairoch, and Cathy H. Wu.
Protein sequence databases.
Current Opinion in Chemical Biology, 8:76-80, 2004.

4

Peter Buneman, Martin Grohe, and Christoph Koch.
Path Queries on Compressed XML.
In Proceedings of the 29th International Conference on Very Large Databases (VLDB), pages 141-152. Morgan Kaufmann, 2003.

5

Giorgio Busatto, Markus Lohrey, and Sebastian Maneth.
Efficient memory representation of xml documents.
In DBPL, 2005.

6

Yi Chen, George A. Mihaila, Rajesh Bordawekar, and Sriram Padmanabhan.
L-tree: A dynamic labeling structure for ordered xml data.
In Wolfgang Lindner, Marco Mesiti, Can Türker, Yannis Tzitzikas, and Athena Vakali, editors, EDBT Workshops, volume 3268 of Lecture Notes in Computer Science, pages 209-218. Springer, 2004.

7

James Cheney.
XMLPPM: XML-Conscious PPM Compression.
See http://www.cs.cornell.edu/People/jcheney/xmlppm/xmlppm.html.

8

Paolo Ferragina, Fabrizio Luccio, Giovanni Manzini, and S. Muthukrishnan.
Compressing and searching xml data via two zips.
In WWW, pages 751-760, 2006.

9

Torsten Grust, Maurice van Keulen, and Jens Teubner.
Accelerating xpath evaluation in any rdbms.
ACM Trans. Database Syst., 29:91-131, 2004.

10

Alan Halverson, Josef Burger, Leonidas Galanis, Ameet Kini, Rajasekar Krishnamurthy, Ajith Nagaraja Rao, Feng Tian, Stratis Viglas, Yuan Wang, Jeffrey F. Naughton, and David J. DeWitt.
Mixed Mode XML Query Processing.
In Proceedings of the 29th International Conference on Very Large Databases (VLDB), pages 225-236. Morgan Kaufmann, 2003.

11

Guy Jacobson.
Succinct Static Data Structures.
PhD thesis, Carnegie Mellon University, 1988.

12

H. V. Jagadish, S. Al-Khalifa, A. Chapman, L. V. S. Lakshmanan, A. Nierman, S. Paparizos, J. M. Patel, D. Srivastava, N. Wiwatwattana, Y. Wu, and C. Yu.
TIMBER: A native XML database.
VLDB Journal, 11(4):274-291, 2002.

13

Vanja Josifovski, Marcus Fontoura, and Attlila Barta.
Querying XML streams.
VLDB Journal, 14(2):197-210, 2005.

14

Jyrki Katajainen and Erkki Makinen.
Tree compression and optimization with applications.
In International Journal of Foundations of Computer Science (FOCS), Vol. 1, pages 425-447. IEEE Computer Society, 1990.

15

Quanzhong Li and Bongki Moon.
Indexing and querying XML data for regular path expressions.
In Proceedings of the 27th International Conference on Very Large Databases (VLDB), pages 361-370. Morgan Kaufmann, 2001.

16

Hartmut Liefke and Dan Suciu.
XMill: an efficient compressor for XML data.
In Proceedings of the 2000 ACM SIGMOD international conference on Management of data, pages 153-164. ACM Press, 2000.

17

Sebastian Maneth and Giorgio Busatto.
Tree transducers and tree compressions.
In Igor Walukiewicz, editor, FoSSaCS, volume 2987 of Lecture Notes in Computer Science, pages 363-377. Springer, 2004.

18

Mitchell P. Marcus, Beatrice Santorini, and Mary Ann Marcinkiewicz.
Building a large annotated corpus of English: the Penn Treebank.
Computational Linguistics, 19, 1993.

19

Jun-Ki Min, Myung-Jae Park, and Chin-Wan Chung.
XPRESS: A Queriable Compression for XML Data.
In Proceedings of the 2003 ACM SIGMOD international conference on Management of data, pages 122-133. ACM Press, 2003.

20

J. Ian Munro, Venkatesh Raman, and Adam J. Storm.
Representing Dynamic Binary Trees Succinctly.
In Proceedings of the 12th Annual Symposium on Discrete Algorithms (SODA), pages 529-536. SIAM, 2001.

21

Adam Silberstein, Hao He, Ke Yi, and Jun Yang.
BOXes: Efficient maintenance of order-based labeling for dynamic XML data.
In the 21st International Conference on Data Engineering (ICDE), pages 285-296, 2005.

22

Pankaj M. Tolani and Jayant R. Haritsa.
XGRIND: A query-friendly XML compressor.
In Proceedings of the 18th International Conference on Data Engineering (ICDE), pages 225-234. IEEE Computer Society, 2002.

23

Ning Zhang, Varun Kacholia, and M. Tamer Ozsu.
A Succinct Physical Storage Scheme for Efficient Evaluation of Path Queries in XML.
In Proceedings of the 20th International Conference on Data Engineering (ICDE), pages 54-65. IEEE Computer Society, 2004.

Footnotes

... parser¹

http://www.sourceforge.net/projects/expat/