Speeding up Adaptation of Web service Compositions using Expiration Times

John Harney

LSDIS Lab, Dept. of Computer Science, University of Georgia
Athens, GA 30602

jfh@cs.uga.edu

Prashant Doshi

LSDIS Lab, Dept. of Computer Science, University of Georgia
Athens, GA 30602

pdoshi@cs.uga.edu

Copyright is held by the World Wide Web Conference Committee (IW3C2). Distribution of these papers is limited to classroom use, and personal use by others.
WWW 2007, May 8-12, 2007, Banff, Alberta, Canada.

ABSTRACT

Web processes must often operate in volatile environments where the quality of service parameters of the participating service providers change during the life time of the process. In order to remain optimal, the Web process must adapt to these changes. Adaptation requires knowledge about the parameter changes of each of the service providers and using this knowledge to determine whether the Web process should make a different more optimal decision. Previously, we defined a mechanism called the value of changed information which measures the impact of expected changes in the service parameters on the Web process, thereby offering a way to query and incorporate those changes that are useful and cost-efficient. However, computing the value of changed information incurs a substantial computational overhead. In this paper, we use service expiration times obtained from pre-defined service level agreements to reduce the computational overhead of adaptation. We formalize the intuition that services whose parameters have not expired need not be considered for querying for revised information. Using two realistic scenarios, we illustrate our approach and demonstrate the associated computational savings.

Categories & Subject Descriptors

H.3.5Information Storage and Retrieval Online Information Services [Web-based Services] G.3 Probability and Statistics[Markov processes]

General Terms

Algorithms, Theory

Keywords

Web services, Adaptation, Volatile environments, Expiration times

1 Introduction

Business environments in which Web services (WS) must function are seldom static. Key characteristics of service providers such as the reliability rate of their services and other quality-of-service parameters, which may affect WS compositions tend to be volatile. As a concrete example, consider a supply chain in which two suppliers compete for orders from a large manufacturer. The sequence in which the manufacturer uses the services of the two suppliers depends on the probability with which the suppliers usually satisfy the orders and the cost of using them. If the preferred supplier's rate of order satisfaction drops suddenly (due to unforeseen circumstances), a cost-conscious manufacturer should replace it with the other supplier to remain optimal.

The key components for maintaining an adaptive Web process - a business process with WSs as its components - are then: $(i)$ up-to-date knowledge of the current parameters of the service providers, and $(ii)$ a measure of the suboptimality of the current Web process. Both these aspects come with their own attendant challenges spanning from how to obtain the new service parameters and from which providers to finding approaches that associate a measure of optimality to the Web process. In addition, if there is a cost to obtaining the new information, not all changes to the Web process composition effected by the revised information may be worth the cost.

Prevalent approaches to automatically composing Web processes use methods within classical planning [13] and decision-theoretic planning [4]. These rely on pre-specified models of the process environment to generate the WS compositions. In [5], Harney and Doshi introduced a mechanism called the value of changed information (VOC) by which the expected impact of the revised information on the Web process could be calculated. The approach involved selectively querying the service providers for their revised parameters. If the change brought about by the revised information was worth the cost of obtaining it, the Web process was reformulated.¹ Thus, the VOC mechanism avoids ``unnecessary'' queries in comparison to the naive approach of, say, periodically querying all the service providers. While this approach results in adaptive Web processes that incur lesser costs in simulated volatile environments [5], computationally the approach turns out to be inefficient.

In this paper, we improve on the previous VOC based approach to adaptation by using the insight that service providers are often able to guarantee that the parameters of their services will persist for some amount of time. Thus, we need not consider querying those service providers for revised information whose previously obtained information has not expired. We incorporate this insight into the VOC formulation, and call the new approach, the value of changed information with expiraton times (VOC $^\mathcal {E}$ ). Because VOC $^\mathcal {E}$ focuses the computations on only those services whose parameters could have changed, it is computationally more efficient than the traditional VOC, while resulting in Web processes that are as cost-efficient in volatile environments as those in the previous approach.

We theoretically show that the adaptation of the Web processes using VOC $^\mathcal {E}$ is as good as the one using VOC and empirically demonstrate that, on average, the approach based on VOC $^\mathcal {E}$ is computationally less intensive. In the worst case, the two approaches exhibit identical asymptotic complexities. For the purpose of empirical evaluation, we utilize two realistic Web process scenarios - a supply chain and a clinical administrative pathway. Within our service-oriented architecture (SOA), we represent the manufacturer's and hospital's Web processes using WS-BPEL [6], and the provider services as well as a service for computing the VOC $^\mathcal {E}$ using WSDL [12].

2 Related Work

Recently, researchers are increasingly turning their attention to managing processes in volatile environments. Au et al. [2] obtain current parameters about the Web process by querying Web service providers when the parameters expire. While this is similar in concept to our approach, plan recomputation is assumed to take place irrespective of whether the revised parameter values are expected to bring about a change in the composition. This may lead to frequent unnecessary computations. In [3], several alternate plans are pre-specified at the logical level, physical level, and the runtime level. Depending on the type of changes in the environment, alternative plans from these three stages are selected. While capable of adapting to several different events, many of the alternative pre-specified plans may not be used making the approach inefficient, and there is no guarantee of optimality of the resulting Web processes. In a somewhat different vein, Verma et al. [11] explore adaptation in Web processes in the presence of coordination constraints between different WSs. We do not consider such constraints here.

In [10], graph based techniques were used to evaluate the feasibility and correctness of changes at the process instance level. Muller et al. [8] propose a workflow adaptation strategy based on pre-defined event-condition-action rules that are triggered when a change in the evironment occurs. While the rules provide a good basis for performing contingency actions, they are limited in the fact that they cannot account for all possible actions and scenarios that may arise in complex workflows. Additionally, the above work does not address long term optimality of process adaptation. Doshi et al. [4] offers such a solution using a technique that manages the dynamism of Web process environments through Bayesian learning. The process model parameters are updated based on previous interactions with the individual Web services and the composition plan is regenerated using these updates. This method suffers from being slow in updating the parameters, and the approach may result in plan recomputations that do not bring about any change in the Web process.

3 Background: Web Process Adaptation Using VOC

Several characteristics of the service providers who participate in a Web process may change during the life-cycle of a process. For example, in a supply chain, the cost of using the preferred supplier's services may increase, and/or the probability with which the preferred supplier meets the orders may reduce. Not all updates of the parameters cause changes in the process composition. Furthermore, the change effected by the revised information may not be worth the cost of obtaining it. In light of these arguments, the VOC-based approach [5] provides a method that will suggest a query, only when the queried information is expected to be sufficiently valuable to obtain.

While the approach is applicable to any model based process composition technique, for the purpose of illustration, a decision-theoretic planning technique is utilized for composing Web processes [4]. Decision-theoretic planners such as MDPs [9] model the process environment, $WP$, using a sextuplet:

$$WP = \langle S,A,T,C,H,s_0 \rangle$$

where $S = \Pi_{i=1}^n X^i$, where $S$ is the set of all possible states factored into a set, $X$, of $n$ variables, $X = \{X^1,X^2,\ldots,X^n\}$, which together indicate the state of the Web process; $A$ is the set of all possible actions representing the WS invocations; $T$ is a transition function, $T: S \times A \rightarrow \Delta(S)$, which specifies the probability measure over the next state given the current state and action, and denotes the uncertain effect of WS invocations on the process; $C$ is a cost function, $C:S \times A \rightarrow \mathbb{R}$, which specifies the cost of invoking each WS from each state; $H$ is the period of consideration over which the composition must be optimal, also known as the horizon, $0<H\leq\infty$; and $s_0$ is the starting state of the process.

The VOC formulation adopts a myopic approach to information revision, in which a single provider is queried at a time for new information. For example, this would translate to asking, say, only the preferred supplier for its current rates of order satisfaction, as opposed to both the preferred supplier and the other supplier, simultaneously. The revised information may change the probability with which the preferred supplier is known to satisfy the order, contained in the transition function.

Let $V_{\pi^*}(s\vert T')$ denote the expected cost of following the optimal policy, $\pi^*$, from the state $s$ when the revised transition function, $T'$ is used. Since the actual revised transition probability is not known unless we query the service provider, computing the VOC involves averaging over all possible values of the revised transition probability, using the current belief distributions over their values. These distributions may be provided by the service providers through pre-defined service-level agreements or they could be learned from previous interactions with the service providers. Let $V_{\pi}(s\vert T')$ be the expected cost of following the original policy, $\pi$ from the state $s$ in the context of the revised model parameter, $T'$. Note that the policy, $\pi$, is optimal in the absence of any revised information. The expected value of change due to the revised transition probabilities is formulated as:

$$\begin{array}{ll} VOC_{T'(\cdot\vert a,s')}(s) =& \int_{\bf p... ...\pi}(s\vert T')\ & - V_{\pi^*}(s\vert T')] d{\bf p}\end{array}$$ (1)

The subscript to $VOC$, $T'(\cdot\vert a,s')$, denotes the revised information inducing the change. Intuitively, Eq. 1 represents how badly, on average, the original policy, $\pi$, performs in the changed environment as formalized by the MDP model with the revised $T'$.

The probability ${\bf p}$ represents a revised probability of transition on performing a particular action, and $Pr(T'(\cdot\vert a,s')= {\bf p})$ represents the belief over the transition probabilities. Notice that in order to calculate the VOC, we must compute the revised values, $V_\pi(s\vert T')$ and $V_{\pi^*}(s\vert T')$, for all possible ${\bf p}$ and average over their difference based on our distribution over ${\bf p}$. Computing $V_\pi(s\vert T')$, which represents the expected cost of following the policy $\pi$ from state $s$ is straightforward since it does not involve the optimization operation over all actions. However, the revised value function $V_{\pi^*}(s\vert T')$ is computed by solving the MDP which may become computationally expensive with large problems.

Analogous to the value of perfect information, VOC is guaranteed to be non-negative at each state of the Web process. For the proof see [5].

Since querying the model parameters and obtaining the revised information may be expensive, we must undertake the querying only if we expect it to pay off. In other words, we query for new information from a state of the Web process only if the VOC due to the revised information in that state is greater than the query cost. More formally, we query if:

$$VOC_{T'(\cdot\vert a,s')}(s) > QueryCost(T'(\cdot\vert a,s'))$$

where $T'(\cdot\vert a,s')$ represents the distribution we want to query.

In order to formulate and execute the Web process, we simply look up the current state of the Web process in the policy and execute the WS prescribed by the policy for that state. The response of the WS invocation determines the next state of the Web process. The composition of the Web process is adapted to fluctuations in the model parameters by interleaving the formulation with VOC computations. The algorithm for the adaptive Web process composition is shown in Fig. 1.

Figure 1: Algorithm for adapting a Web process to revised information and executing it.

Algorithm for adaptive Web process


Input:  $\pi^*$ //optimal policy, $s_0$ //initial state 



$s \leftarrow s_0$


while goal state not reached


if VOC$^*$(s) $>$ QueryCost
$(T'(\cdot\vert a,s'))$ 


Query service provider, $a^*$ (Eq. 2), for


new probabilities 


Form the new transition function, $T'$ 


Calculate policy $\pi^*$ using the new MDP model


with $T'$ 



$a \leftarrow \pi^*(s)$


Execute the Web service $a$


Get response of $a$ and construct next state, s'



$s \leftarrow s'$


end while


end algorithm

For each state encountered during the execution of the Web process, a service provider is queried for new information if the query is expected to bring about a change in the Web process that exceeds the query cost. For example, in the supply chain process, we select and query a supplier for its current rate of order satisfactions. Of all the suppliers, we select the one whose possible new rate of order satisfaction is expected to bring about the most change in the Web process, and this change exceeds the cost of querying that provider. In other words, we select the service provider associated with the WS invocation, $a^*$, to possibly query for whom the VOC is maximum:

$$VOC^*(s) = \underset{a \in A}{max}   VOC_{T(\cdot\vert a,s')}(s)$$ (2)

Thus, $a^* = \underset{a \in A}{argmax}   VOC_{T(\cdot\vert a,s')}(s)$

Calculating the VOC$^*$ as shown in Eq. 2 is computationally intensive. It involves iterating over all the service providers and computing the VOC for each. Because there could be many service providers participating in the Web process, a more selective approach is needed to obtain computational efficiency. We present one such method next.

4 Motivating Scenarios

In order to illustrate our approach we present two example scenarios:

MS XBox 360 Supply Chain Our first scenario is a simplified version of the supply chain employed by Microsoft (MS) for the production of its XBox 360 gaming console [7]. MS engages a variety of suppliers and contract manufacturers to deliver the components that are crucial to the production of the gaming console. Because MS outsources key manufacturing operations, it needs to retain tight control over those external processes to ensure that the suppliers and contract manufacturers meet service level agreements.

Figure 2: Interactions between the business partners in the Microsoft XBox 360 supply chain. We have used example probability values to aid understanding.

In Fig. 2, we focus on a simplified supply chain scenario in which MS chooses a contracted console manufacturer, resonsible for assembling the console, and a contracted graphics processing unit (GPU) manufacturer who is responsible for building the advanced GPU chips. We assume that the invocations will be carried out in a sequential manner, beginning with the GPU followed by the console. ² We assume that each of the manufacturers has the option to order their components from three different suppliers. They may order from a preferred supplier with which they usually interact. The manufacturers may also order the parts from other suppliers or resort to the spot market. A costing analysis reveals that the least cost will be incurred if the order is satisfied by the preferred supplier. They will incur increasing costs as they try to fulfill the orders by procuring the console and GPU chips from another supplier and the spot market.

Clearly, MS and its manufacturers must choose from several candidate processes. For example, they may initially attempt to satisfy the order of GPU chips from the preferred supplier. If the preferred supplier is unable to satisfy the order, MS may resort to ordering parts from some other supplier. Another potential process may involve bypassing the preferred supplier, since MS strongly believes that the preferred supplier will not satisfy the order. It may then initiate a status check on some other supplier. These example processes reveal two important factors for selecting the optimal one. First, MS must accurately know the certainty with which the console and GPU chip orders will be satisfied by each of its supplier choices. Second, at each stage, rather than greedily selecting an action with the least cost, MS must select the action which is expected to be optimal over the long term.

Patient Transfer A hospital receives a patient who has complained of a particular ailment. The patient is first checked into the hospital and then seen by one of the hospital's physicians. He may, upon examination, decide to transfer the patient to a secondary care provider for specialist treatment. For this example, we assume that the hospital has a choice of four secondary care givers to select from with differing vacancy rates and costs of treatment, with the preferred one having the best vacancy rate and least cost (see Fig. 3).

Similar to our previous example, several candidate Web processes present themselves. For example, the physician may decide not to transfer the patient, instead opting for in-house treatment. However, if the physician concludes that specialist treatment is required, several factors weigh in toward selecting the secondary care giver. These include, the typical vacancy rates of the care givers, costs of treatment, and geographic proximity.

Figure 3: The patient transfer clinical pathway for a primary caregiver. As before, we have used example probability values to aid understanding.

The process flows in both the supply chain and the patient transfer scenarios hinge on the rates of order satisfaction and vacancy rates, respectively. If the order satisfaction rate of the preferred supplier or the vacancy rate of the preferred secondary caregiver drops, the processes need to be adapted to remain cost-effective.

5 VOC $^{\mathcal {E}}$: VOC with Expiration Times

As we mentioned previously, in order to select a service provider for querying for revised information, the previous approach [5] required iterating over all the WSs and selecting the one which results in the largest VOC. For large Web processes, there could be several participating WSs, making the process of selection computationally intensive.

To address this challenge, we use the insight that service providers are often able to guarantee that their reliability rates and other quality-of-service parameters will remain fixed for some time, $t_{exp}$, after which they may vary. WS providers may define $t_{exp}$ in a WS-Agreement document [1] as we show later.

Given a way to keep track of guarantees of which WSs have expired, we may compute the VOC for only those service providers whose guarantees have expired and select among them. This is because a possible query to the others will return back parameter values that are unchanged from those used in formulating the current Web process. Thus such queries will cause no adaptation in the Web process, and may be safely ignored.

1 Definition

In keeping with [5], we adopt a myopic approach to information revision, in which we query a single provider at a time for new information. To keep matters simple, we assume that the service providers will be queried for their current rates (probabilities) with which they are able to satisfy their incoming orders or requests. This new information may cause a change in the transition function of the model of the process environment, as shown in Section 3.

In a departure from [5], we assume that, in addition to providing their current reliability rates, the service providers also give the duration of time for which the current reliability rates are guaranteed to remain unchanged. We call this duration as the expiration time of the revised information. Let $a$ represent the action of invoking the WS, $WS^a$, $\mathcal{E}$ be the current set of actions representing the invocations of WSs whose guarantees have expired, then we define the maximum VOC, VOC $^\mathcal {E}$, as:

$$VOC^\mathcal{E}(s) = \underset{a \in \mathcal{E}}{max}   VOC_{T(\cdot\vert a,s')}(s)$$ (3)

where $VOC_{T(\cdot\vert a,s')}(s)$ is as defined in Eq. 1, and we note that $\mathcal{E} \subseteq A$. In the worst case, $\mathcal{E} = A$, and all WSs have expired, in which case, VOC $^\mathcal {E}$ collapses to VOC$^*$ defined in Eq. 2. In the best case, $\mathcal{E} = \phi$, and none of the WSs have expired, in which case VOC $^\mathcal {E}$ = 0.

The challenge then is to correctly maintain the set, $\mathcal{E}$, during the lifetime of the Web process; we show one such way of doing this next.

2 Algorithm

Figure 4: Algorithm for adaptive Web process using VOC $^\mathcal {E}$.

In Fig. 4, we show the algorithm for generating, executing, and adapting the Web process to a volatile environment using VOC $^\mathcal {E}$. The algorithm takes as input the initial state of the process, and a policy, $\pi^*$, obtained by solving the process model (Section 3), which prescribes which WS to invoke from each state of the process.

As we mentioned before, we associate with each WS$^a$ participating in the process, an expiration time, $t_{exp}^{T(.\vert a,s')}$, during which the parameters of the WS such as its reliability are guaranteed to be fixed. We begin by checking which of the WSs have expired guarantees (lines 5-10) and updating the set, $\mathcal{E}$, with those that have expired. The next step is to compute VOC $^\mathcal {E}$ (Eq. 3), which will suggest a service provider among the expired set, $\mathcal{E}$, to query for revised information that is expected to bring about most change in the Web process.

Figure 5: Anticipating Web services that will expire while computing VOC $^\mathcal {E}$.

Notice that a WS might expire while computing VOC $^\mathcal {E}$. We must anticipate this and add those services in advance to the set, $\mathcal{E}$, so that they are taken under consideration while computing VOC $^\mathcal {E}$. In line 8, the algorithm invokes the procedure in Fig. 5, which finds out which WSs among the unexpired ones (denoted by $\bar{\mathcal{E}}$) may expire while computing VOC $^\mathcal {E}$ and adds these to the set $\mathcal{E}$. We note that if a WS is added to $\mathcal{E}$, the time taken to compute VOC $^\mathcal {E}$ may increase, during which other WSs may expire. We consider this by recursively invoking the procedure until no more WSs are added to the set, $\mathcal{E}$. The time taken to compute VOC $^\mathcal {E}$, $t_{VOC^\mathcal{E}(s)}$, needs to be anticipated; if $t_{VOC(s)}$ is the time taken to compute the VOC (Eq. 1), then $t_{VOC^\mathcal{E}(s)} = \vert\mathcal{E}\vert t_{VOC(s)}$. Notice that $t_{VOC(s)}$ is fixed and may be obtained a'priori.

If VOC $^\mathcal {E}$ exceeds the cost of querying the service provider, then we query the provider for the new reliability rates, which form the new $T'$ in the process model. We also add the time taken to perform the VOC $^\mathcal {E}$ calculations to the cumulative time counter associated with each WS (lines 11-15). On querying, in addition to obtaining the possibly revised information, we also obtain the new expiration times for the information. Thus, the counter for the WS that is queried is reset.

Figure 6: Time elapsed in querying a service provider for revised information, $t_{QLag}$

We observe that querying for information is not a constant time step operation, but must take into account the time taken for the request to reach the provider, the provider's information-providing WS to complete its computations, and for the the response to arrive back at the process. We denote the total time consumed in querying as $t_{QLag}$, which is depicted in Fig. 6.

The revised information is integrated into the process model and a new policy is recomputed to maintain optimality of the Web process. However, recomputation of the policy is not always necessary, and runtime changes could be made to the process. Here, the time counters must be updated again to account for the time taken to recalculate the policy. Finally, the queried WS is removed from $\mathcal{E}$ (lines 21-26). We observe that the times, $t_{QLag}$ and $t_{\pi^*}$ could be calculated in real-time (online) using timestamps before and after the calcuations.

Figure 7: Time elapsed in obtaining a response to service invocation, $t_{Response}$.

Of course, if the query cost exceeds $VOC^{\mathcal{E}}$, then we ignore the previously mentioned steps, and simply invoke the WS that the original policy recommends. Obtaining a response from the invoked WS may not be a constant time operation but may depend on external factors, as shown in Fig. 7. Let $t_{Response}$ be the time elapsed, then this time is added to all the cumulative time counters (lines 28-33).

3 Theoretical Results

We first show that given an identical input, adaptation using VOC $^\mathcal {E}$ results in the same set of Web processes as compared to adaptation using VOC$^*$ [5].

Proposition 1 (Correctness) Given identical policies and start states, adaptation using VOC $^\mathcal {E}$ and VOC$^*$ generate identical Web processes.

Proof. We begin with the definition of VOC$^*$ (Eq. 2):

$$\begin{array}{ll} VOC^*(s) & = \underset{a \in A}{max} VOC_{T... ...\bar{\mathcal{E}}}{max} VOC_{T(\cdot\vert a,s')}(s) \end{array}$$

where $\bar{\mathcal{E}}$ is the complement of $\mathcal{E}$ as mentioned previously.

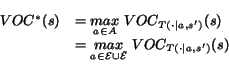
We consider two cases: $(i)$ If the WS with the maximum VOC selected for querying has expired, $a^* \in \mathcal{E}$, then VOC$^*$ = VOC $^\mathcal {E}$ for every state, and the Web process will be adapted identically to when VOC $^\mathcal {E}$ is used. On the other hand, $(ii)$ if the WS associated with the maximum VOC has not expired, then since the revised information is guaranteed to be unchanged, VOC$^*$ = 0, and the Web process also remains unchanged. Thus, for both the cases, the resulting Web process will be identical to the one generated when VOC $^\mathcal {E}$ is used. $\qedsymbol$

We derive the worst case complexity of the adaptation next. While the worst case complexity is similar to the complexity of adaptation using VOC$^*$, on average we expect significant computational gains from considering expiration times. We demonstrate these gains experimentally in the next section. A theoretical analysis of the average case complexity of this approach is part of our future work.

Proposition 2 (Complexity) Let $N$ denote the number of possible values a given random variable $X$ can take. The worst case complexity of adaptation using VOC $^\mathcal {E}$, as performed by the algorithm shown in Fig. 4, is:

$$\begin{array}{ll} \mathcal{O}(N^{\vert X\vert} (N^{2\vert X\v... ...t A\vert^2\vert H\vert + t_{QLag} + t_{Response})). \end{array}$$

Proof. We refer to the algorithm for adaptation using VOC $^\mathcal {E}$ shown in Figure 4. The outer while loop (line 4) will terminate when a goal state is reached. If $\vert X\vert$ is the number of variables with maximum value $N$, the largest size of the state space is $N^{\vert X\vert}$. In the worst case, we will traverse every possible state in the process with the last possible state reached being the goal state, and will thus the execute the loop $N^{\vert X\vert}$ times.

Within the body of the loop we focus on three operations in particular. First, lines 5-10 update the set of expired services, $\mathcal{E}$. Here, a loop iterates over all WSs (ie,$\vert A\vert$) effectively having an execution time in the order of $\mathcal{O}(\vert A\vert)$. However, each pass of the loop calls the AddExpiredServices procedure (Fig 5), which terminates when no more services are added to $\mathcal{E}$. In the worst case, this procedure will add one service to $\mathcal{E}$, and then $t_{VOC^\mathcal{E}}$ will increase such that one more service will expire, in which case another service will be added to $\mathcal{E}$; this process is repeated until all the services are added. We may then write the following recurrence for the runtime of this procedure:

$$T(\vert A\vert) = \mathcal{O}(\vert A\vert) + T(\vert A\vert-1)$$ (4)

Equation 4 shows that each pass of the loop will take $\mathcal{O}(\vert A\vert)$ and, in the worst case, one service will be added to $\mathcal{E}$ for each pass. On solving, this recurrence will run in $\mathcal{O}(\vert A\vert^2)$ time. Subsequently, lines 5-10 will take $\mathcal{O}(\vert A\vert^3)$. Second, line 10 involves a calculation of VOC $^\mathcal {E}$, which in the worst case collapses to a VOC$^*$ calculation (when all services have expired). VOC$^*$, as mentioned in Equation 2, is the maximum VOC over all services involved in the process, so $\vert A\vert$ VOC calculations are required. Each VOC calculation involves a comparison between values produced by the optimal policy and the current policy in the changed environment. Finding the optimal policy of a process takes $\mathcal{O}(N^{2\vert X\vert}\vert A\vert\vert H\vert)$ time, where $\vert H\vert$ represents the length of the horizon (Similarly, recalculation of the policy in line 22 will also take this time). In total, VOC $^\mathcal {E}$ will run in $\mathcal{O}(N^{2\vert X\vert}\vert A\vert\vert H\vert)$ time. Finally, we must also consider $t_{QLag}$ (line 19) and $t_{response}$ (line 32), as these are external to the process and independent of the VOC calculations.

Thus the total runtime complexity is:

$$\begin{array}{llll} \mathcal{O}(VOC^{\mathcal{E}}) = & \mathc... ...mathcal{O}(N^{\vert X\vert}\times t_{Response}) \ \end{array}$$

We can eliminate the second term because

$$\begin{array}{ll} & N^{2\vert X\vert} » \vert A\vert\ \end{array}$$

So now we are left with the following complexity:

$$\begin{array}{llll} \mathcal{O}(VOC^{\mathcal{E}}) = & \mathc... ...mathcal{O}(N^{\vert X\vert}\times t_{Response}) \ \end{array}$$

which may be rewritten as:

$$\begin{array}{ll} \mathcal{O}(N^{\vert X\vert} (N^{2\vert X\v... ...rt A\vert^2\vert H\vert + t_{QLag} + t_{Response})) \end{array}$$

$\qedsymbol$

6 Experiments

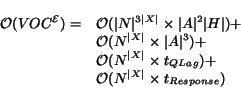
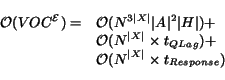
We first outline our SOA in which we wrap the VOC $^\mathcal {E}$ computations in WSDL based internal Web services, followed by our experimental results on the performance of the adaptive Web process as compared to the previous approach.

1 Architecture

The algorithm described in Fig. 4 is implemented as a WS-BPEL [6] flow while all WSs were implemented using WSDL [12]. To the WS-BPEL flow, we give the optimal policy, $\pi^*$, and the start state as input. Our experiments utilized IBM's BPWS4J engine for executing the BPEL process and AXIS 2.0 as the container for the WSs. We show our SOA in Fig. 8.

Figure 8: SOA for implementing our adaptive Web process.

Within our SOA, we provide internal WSs for solving the MDP model of the Web process and generating the policy, and computing the VOC $^\mathcal {E}$. If the VOC $^\mathcal{E}(s)$ exceeds the cost of querying a particular service provider (this cost is also provided as an input), the WS-BPEL flow invokes a special WS whose function is to query the service provider's information-providing WSs for revised information and the new expiration times. This information is used to formulate and solve a new MDP and the output policy is fed back to the WS-BPEL flow. This policy is used by the WS-BPEL flow to invoke the prescribed external WS and the response is used to formulate the next state of the process. This procedure continues until the goal state is reached.

2 Performance Evaluation

The objective of our experimental evaluation is three-fold: $(i)$ We show the utility of adapting to a (simulated) volatile environment by comparing against Web processes that do not adapt and use a fixed policy during execution; $(ii)$ By being intelligent in selecting which service provider to query, we show that adaption using VOC $^\mathcal {E}$ results in Web processes that incur less average costs as compared to an approach that randomly selects a service provider to query at randomly selected states of the process; and $(iii)$ the average execution time of the Web process adapted using VOC $^\mathcal {E}$ is less than when the process is adapated using VOC$^*$ [5], and varies intuitively as the expiration times vary.

Figure 9: An example WS-Agreement document showing the agreed upon expiration time and the rate of order satisfaction of a supplier for the XBox supply chain.

Figure 10: The probability density functions representing $(a)$ MS's belief over the GPU and console suppliers' rates of order satisfaction in the XBox supply chain scenario; $(b)$ the primary caregiver's beliefs over the secondary caregivers' probabilities of having a vacancy.

MS XBox Supply Chain

$(a)$

Patient Transfer Pathway

$(b)$

We utilized the MS XBox supply chain and the clinical patient transfer scenarios (Section 4) for our evaluations. For the supply chain example, we queried the suppliers for their current percentage of order satisfaction while in the patient transfer pathway, we queried the secondary caregivers for their current vacancy rates.³ In addition to the revised information about their services, the providers also guarantee a duration over which the WS parameter values will remain fixed. ⁴ These distributions may be provided by the service providers using service-level agreements drawn up using, say, the WS-Agreement specification [1]. Figure 9 shows a part of the agreement between MS and the preferred GPU supplier in the XBox scenario. $t_{exp}$ is defined within the $<ExpirationTime>$ subtag of the $<Context>$ tag. Here, the entire agreement will expire on January 27, 2007. Further in the document, the $<ServiceDescriptionTerm>$ subtag of the $<Terms>$ tag defines the provider's rate of GPU order satisfaction (probability of 0.4). Thus, MS and the contracted GPU manager have agreed that any order of GPUs from MS will be satisfied 40 percent of the time until the agreement is voided on January 27, 2007.

For the service providers when their information has expired, we model the manufacturer and primary caregiver's beliefs over their possible parameter values, ( $Pr(T'(\cdot\vert a,s')={\bf p}$) in Eq. 1) using beta density functions. Other density functions such as Gaussians or polynomials may also be used. Fig. 10$(a)$ shows the beta densities that represent Microsoft's distribution over the rate of order satisfaction by the GPU contract manufacturer ie. $T'$( $\textbf{Preferred Supplier}$ $\textbf{Avail.}=Yes$ $\vert$ $\textsf{Check Preferred Supplier}$, $\textbf{Preferred}$
$\textbf{Supplier Avail.}=Unknown$), and analogously for the other suppliers (the Spot Market is assumed to always be available at a rate of 100 percent). Means of the densities reveal that the preferred suppliers of both the GPUs and consoles tend to be less reliable in satisfying orders than other suppliers. Fig. 10$(b)$ shows the density plots over the probability of a vacancy with the preferred and other secondary caregivers. For those service providers whose revised information has not expired, the manufacturer and caregiver's beliefs could be seen as Dirac-delta functions, with the non-zero value fixed at the probability, ${\bf p}$, that was provided at the time of query. Thus, for this case, the $VOC(s) = 0$ at any state of the process. We emphasize that these densities are marginalizations of the more complex plots that would account for all the factors that may influence a supplier's ability to satisfy an order, such as the time that an order is placed and quantity of the order.

Figure 11: $(a)$ A comparison of the average process costs incurred when using VOC $^\mathcal {E}$ based adaption with a strategy of random adaption and no adaptation. $(b)$ Average process execution times when using the VOC $^\mathcal {E}$ based adaptation, VOC$^*$ based adaptation and no adaptation. $(c)$ and $(d)$ show analogous results for the patient transfer clinical pathway.

MS XBox Supply Chain

$(a)$

$(b)$

Patient Transfer Clinical Pathway

$(c)$

$(d)$

In order to perform the evaluations, we simulated a volatile business environment for each of the two problem domains. For the supply chain, the rates of order satisfaction for the preferred and other suppliers were assumed to vary according to the density plots in Fig. 10. The expiration times were upper bound to a large time interval and randomly selected within the bound. The rates of order satisfaction remained fixed until the corresponding expiration times elapsed, after which, on query, new expiration times were randomly selected. Other parameters of the environment such as the WS invocation costs, $t_{QLag}$, and $t_{Response}$, are as given in the Table 1. The environment for the patient transfer problem was simulated analogously (see Table 2).

Table 1: Costs, $t_{QLag}$, and $t_{Response}$ for the WSs in the supply chain scenario.

Service	Cost	$t_{QLag}$(s)	$t_{Response}$(s)
GPUPreferredSupplier	40	1	5
GPUOtherSupplier	70	1	4
GPUSpotMarket	130	1	3
ConsolePreferredSupplier	40	1	5
ConsoleOtherSupplier	70	1	4
ConsoleSpotMarket	130	1	3

Table 2: Costs, $t_{QLag}$, and $t_{Response}$ for the services in the patient transfer scenario.

Service	Cost	$t_{QLag}$(s)	$t_{Response}$(s)
PatientCheckIn	10	1	1
InsuranceValidation	10	1	1
PhysicalExam	10	1	2
PreferredSecondaryCaregiver	20	1	3
SecondaryCaregiver2	40	1	3
SecondaryCaregiver3	60	1	3
SecondaryCaregiver4	200	1	3

In Figs. 11$(a)$ and $(c)$, we compare three strategies of adaptation with respect to the average cost incurred from the execution of the Web process, as the cost of querying the service providers is increased. These strategies include no adaptation and keeping the policy fixed, randomly selecting a single service provider at randomly selected states of the process, and adapting the Web process using VOC $^\mathcal {E}$. Our methodology consisted of running 100 independent instances of each process within the simulated volatile environment and plotting the average cost of executing the process for different query costs. We ensured that the processes using each of the three strategies received similar responses from the service providers, and the expiration times were kept fixed.

We note that these results are analogous to those reported in [5] for VOC$^*$ and they show that the Web process incurs lower average costs when adapted using VOC $^\mathcal {E}$, thereby establishing the utility of sophisticated adaptation in volatile environments. In particular, as we increase the cost of querying, our VOC $^\mathcal {E}$ based approach performs less queries and adapts the Web process less. For large query costs, its performance approaches that of a Web process with no adaptation because costly queries for revised information are not worth the possible change in the cost of the process due to adaptation. For smaller query costs, a VOC based approach will query frequently, though not as much as a strategy that always queries a random provider.

In Figs. 11$(b)$ and $(d)$, we compare the runtimes taken in generating and executing the Web process. We compare the execution time of a process without any adaptation (see [4] for the algorithm), with the execution time of a process adapted using VOC$^*$ [5], and the execution time of a process adapted using VOC $^\mathcal {E}$ (Fig. 4). As we increase the expiration times associated with the revised information obtained from the providers, the process execution time when adapted using VOC $^\mathcal {E}$ decreases. Notice that it is upper bounded by the execution times of a process adapted using VOC$^*$ and lower bounded by the runtimes of a process with no adaptation. This is intuitive because VOC$^*$ always involves considering all participating WSs for querying, while no such computations are carried out in a process that does not adapt. Both these execution times are invariant with respect to the expiration times. Our results demonstrate the inverse relationship between expiration times and computational effort expended on adaptation.

Our experiments provide two conclusions: First, by augmenting Web process composition with VOC based calculations, significant information changes in volatile environments are considered and used to make better decisions about which services to invoke next. The comparison of VOC $^\mathcal {E}$ and static policy implementations illustrate that the overall average cost of the Web process when adapted is significantly less than utilizing a non-changing policy. Second, we demonstrated that if service providers are able to provide longer guarantees on their service reliability, less computational effort needs to be spent on adapting the Web processes. This substantiates the intuition that in less volatile environments as formalized by higher expiration times, less adaptation is required to keep the Web process optimal.

7 Conclusion

Business environments seldom remain unchanged over the lifetime of a Web process. While the environment may change in several ways, we considered changes in the quality-of-service parameters such as rates of order satisfaction in this paper. Prevalent approaches to WS composition utilize a pre-specified model of the process environment to formulate the Web process. However, in a dynamic process environment the model may change over time. We presented a method that intelligently adapts a Web process to changes in parameters of service providers, thereby incurring less costs. While this approach is cost-effective, it may get computationally intensive. Improving on previous work, we showed how service parameter guarantees in the form of expiration times may be used to reduce the computational burden of adaptation. Using two disparate problem domains, we empirically demonstrated the speedups obtained in executing and adapting a Web process to changes in service parameters when using a method that is cognizant of expiration times in comparison to an adaptation strategy that ignores them.

Our future work involves investigating ways in which the volatility of a process environment may be measured and formalised. A formal model of the volatility of a process environment will enable the development of more efficient approaches for adaptation.

REFERENCES

[1] A. Andrieux, K. Czajkowski, A. Dan, K. Keahey, H. Ludwig, T. Nakata, J. Pruyne, J. Rofrano, S. Tuecke, and M. Xu.
WS-Agreement Specification, 2005.

[2] T.-C. Au, U. Kuter, and D. S. Nau.
Web service composition with volatile information.
In International Semantic Web Conference, pages 52-66, 2005.

[3]G. Chafle, K. Dasgupta, A. Kumar, S. Mittal, and B. Srivastava.
Adaptation in web service composition and execution.
In International Conference on Web Services (ICWS), Industry Track, 2006.

[4]P. Doshi, R. Goodwin, R. Akkiraju, and K. Verma.
Dynamic workflow composition using markov decision processes.
Journal of Web Services Research (JWSR), 2(1):1-17, 2005.

[5]J. Harney and P. Doshi.
Adaptive web processes using value of changed information.
In International Conference on Service-Oriented Computing (ICSOC), pages 179-190, 2006.

[6] IBM.
Business Process Execution Language for Web Services version 1.1, 2005.

[7] Enabling an adaptable, aligned, and agile supply chain with biztalk server and rosettanet accelerator.
Technical Report http:// www.microsoft.com / technet / itshowcase /content / scmbiztalktcs.mspx, 2005.

[8] R. Muller, U. Greiner, and E. Rahm.
Agentwork: a workflow system supporting rule-based workflow adaptation.
Journal of Data and Knowledge Engineering., 51(2):223-256, 2004.

[9] M. L. Puterman.
Markov Decision Processes.
John Wiley & Sons, NY, 1994.

[10] M. Reichert and P. Dadam.
Adeptflex-supporting dynamic changes of workflows without losing control.
Journal of Intelligent Information Systems, 10(2):93-17, 1998.

[11] K. Verma, P. Doshi, K. Gomadam, J. Miller, and A. Sheth.
Optimal adaptation in web processes with coordination constraints.
In International Conference on Web Services (ICWS), 2006.

[12] Web Services Description Language (WSDL) 1.1, 2001.

[13] D. Wu, B. Parsia, E. Sirin, J. Hendler, and D. Nau.
Automating daml-s web services composition using shop2.
In International Semantic Web Conference, 2003.

Footnotes

... reformulated.¹

In general, new information may require a complete recomposition of the Web process to remain optimal, though sometimes only local changes may be sufficient.

... console.²

Notice that the process may also be run in parallel.

... rates.³

Of course, the rate of order satisfaction in the supply chain, for example, would depend on the quantity of the order and other factors; we assume that these will be provided to the suppliers.

... fixed.⁴

In the real world, an example response by a supplier to a query could be, ``We will guarantee meeting 2 of every 3 orders for the next six months''.