After the data and ontology layers of the Semantic Web stack have achieved a certain level of maturity in standard recommendations such as RDF and OWL, the query and the rules layers seem to be the next building-blocks to be finalized. For the first part, SPARQL [18], W3C's proposed query language, seems to be close to recommendation, though the Data Access working group is still struggling with defining aspects such as a formal semantics or layering on top of OWL and RDFS. As for the second part, the RIF working group 2, who is responsible for the rules layer, is just producing first concrete results. Besides aspects like business rules exchange or reactive rules, deductive rules languages on top of RDF and OWL are of special interest to the RIF group. One such deductive rules language is Datalog, which has been successfully applied in areas such as deductive databases and thus might be viewed as a query language itself. Let us briefly recap our starting points:
Datalog and SQL. Analogies between Datalog and relational query languages such as SQL are well-known and -studied. Both formalisms cover UCQ (unions of conjunctive queries), where Datalog adds recursion, particularly unrestricted recursion involving nonmonotonic negation (aka unstratified negation as failure). Still, SQL is often viewed to be more powerful in several respects. On the one hand, the lack of recursion has been partly solved in the standard's 1999 version [20]. On the other hand, aggregates or external function calls are missing in pure Datalog. However, also developments on the Datalog side are evolving and with recent extensions of Datalog towards Answer Set Programming (ASP) - a logic programming paradigm extending and building on top of Datalog - lots of these issues have been solved, for instance by defining a declarative semantics for aggregates [9], external predicates [8].
The Semantic Web rules layer. Remarkably, logic programming dialects such as Datalog with nonmonotonic negation which are covered by Answer Set Programming are often viewed as a natural basis for the Semantic Web rules layer [7]. Current ASP systems offer extensions for retrieving RDF data and querying OWL knowledge bases from the Web [8]. Particular concerns in the Semantic Web community exist with respect to adding rules including nonmonotonic negation [3] which involve a form of closed world reasoning on top of RDF and OWL which both adopt an open world assumption. Recent proposals for solving this issue suggest a ``safe'' use of negation as failure over finite contexts only for the Web, also called scoped negation [17].
The Semantic Web query layer - SPARQL. Since we base our considerations in this paper on the assumption that similar correspondences as between SQL and Datalog can be established for SPARQL, we have to observe that SPARQL inherits a lot from SQL, but there also remain substantial differences: On the one hand, SPARQL does not deal with nested queries or recursion, a detail which is indeed surprising by the fact that SPARQL is a graph query language on RDF where, typical recursive queries such as transitive closure of a property might seem very useful. Likewise, aggregation (such as count, average, etc.) of object values in RDF triples which might appear useful have not yet been included in the current standard. On the other hand, subtleties like blank nodes (aka bNodes), or optional graph patterns, which are similar but (as we will see) different to outer joins in SQL or relational algebra, are not straightforwardly translatable to Datalog. The goal of this paper is to shed light on the actual relation between declarative rules languages such as Datalog and SPARQL, and by this also provide valuable input for the currently ongoing discussions on the Semantic Web rules layer, in particular its integration with SPARQL, taking the likely direction into account that LP style rules languages will play a significant role in this context.
Although the SPARQL specification does not seem 100% stable at the current point, just having taken a step back from candidate recommendation to working draft, we think that it is not too early for this exercise, as we will gain valuable insights and positive side effects by our investigation. More precisely, the contributions of the present work are:
The remainder of this paper is structured as follows: In Sec. 2 we first overview SPARQL, discuss some issues in the language (Sec. 2.1) and then define its formal semantics (Sec. 2.2). After introducing a general form of Datalog with negation as failure under the answer set semantics in Sec. 3, we proceed with the translations of SPARQL to Datalog in Sec. 4. We finally discuss the above-mentioned language extensions in Sec. 5, before we conclude in Sec. 6.
In examples, we will subsequently refer to
the two RDF graphs in Fig. 1 which
give some information about ![]() and
and ![]() .
Such information is common in FOAF files which are gaining
popularity to describe personal data. Similarities with existing
examples in [18] are on
purpose. We assume the two RDF graphs given in TURTLE [2] notation and accessible via
the IRIs ex.org/bob and alice.org3
.
Such information is common in FOAF files which are gaining
popularity to describe personal data. Similarities with existing
examples in [18] are on
purpose. We assume the two RDF graphs given in TURTLE [2] notation and accessible via
the IRIs ex.org/bob and alice.org3
|
We assume the pairwise disjoint, infinite sets ![]() ,
, ![]() ,
, ![]() and
and ![]() , which denote IRIs,
Blank nodes, RDF literals, and variables respectively. In this
paper, an RDF Graph is then a finite set, of triples from
, which denote IRIs,
Blank nodes, RDF literals, and variables respectively. In this
paper, an RDF Graph is then a finite set, of triples from
![]() ,4
dereferenceable by an IRI. A SPARQL query is a quadruple
,4
dereferenceable by an IRI. A SPARQL query is a quadruple
![]() , where
, where
![]() is a result form,
is a result form,
![]() is a graph pattern,
is a graph pattern,
![]() is a dataset, and
is a dataset, and
![]() is a set of solution
modifiers. We refer to [18] for syntactical details and
will explain these in the following as far as necessary. In this
paper, we will ignore solution modifiers mostly, thus we will
usually write queries as triples
is a set of solution
modifiers. We refer to [18] for syntactical details and
will explain these in the following as far as necessary. In this
paper, we will ignore solution modifiers mostly, thus we will
usually write queries as triples
![]() , and will
use the syntax for graph patterns introduced below.
, and will
use the syntax for graph patterns introduced below.
The query from Fig. 1 with result
form
![]() then
has solution tuples
then
has solution tuples
![]() ,
,
![]() ,
,
![]() . We write
substitutions in sqare brackets, so these tuples correspond to
the substitutions
. We write
substitutions in sqare brackets, so these tuples correspond to
the substitutions
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() ,
,
![]() ,
respectively.
,
respectively.
The relation between names and graphs in SPARQL is defined
solely in terms of that the IRI defines a resource which is
represented by the respective graph. In this paper, we assume
that the IRIs represent indeed network-accessible resources where
the respective RDF-graphs can be retrieved from. This view has
also be taken e.g. in [17]. Particularly,
this treatment is not to be confused with so-called named graphs
in the sense of [4].
We thus identify each IRI with the RDF graph available at this
IRI and each set of IRIs with the graph merge [13] of the respective IRIs.
This allows us to identify the dataset by a pair of sets of IRIs
![]() with
with
![]() and
and
![]() denoting the (merged) default graph and the set of named graphs,
respectively. Hence, the following set of clauses
denoting the (merged) default graph and the set of named graphs,
respectively. Hence, the following set of clauses
First, note that the default graph if specified by name in a
FROM clause is not counted among the named graphs
automatically [18,
section 8, definition 1]. An unbound variable in the GRAPH
directive, means any of the named graphs in ![]() , but does NOT
necessarily include the default graph.
, but does NOT
necessarily include the default graph.
Some more remarks are in place concerning FILTER
expressions. According to the SPARQL specification ``Graph
pattern matching creates bindings of variables [where] it is
possible to further restrict solutions by constraining the
allowable bindings of variables to RDF Terms [with FILTER
expressions].'' However, it is not clearly specified how to
deal with filter constraints referring to variables which do not
appear in simple graph patterns. In this paper, for graph
patterns of the form
![]() we tacitly assume safe
filter expressions, i.e. that all variables used in a filter
expression
we tacitly assume safe
filter expressions, i.e. that all variables used in a filter
expression ![]() also appear in the
corresponding pattern
also appear in the
corresponding pattern ![]() . This
corresponds with the notion of safety in Datalog (see
Sec.3), where the built-in predicates
(which obviously correspond to filter predicates) do not suffice
to safe unbound variables.
. This
corresponds with the notion of safety in Datalog (see
Sec.3), where the built-in predicates
(which obviously correspond to filter predicates) do not suffice
to safe unbound variables.
Moreover, the specification defines errors to avoid mistyped comparisons, or evaluation of built-in functions over unbound values, i.e. ``any potential solution that causes an error condition in a constraint will not form part of the final results, but does not cause the query to fail.'' These errors propagate over the whole FILTER expression, also over negation, as shown by the following example.
We will take special care for these errors, when defining the semantics of FILTER expressions later on.
We denote by
![]() the union
the union
![]() , where
, where
![]() is a
dedicated constant denoting the unknown value not appearing in
any of
is a
dedicated constant denoting the unknown value not appearing in
any of ![]() or
or ![]() , how it is commonly
introduced when defining outer joins in relational algebra.
, how it is commonly
introduced when defining outer joins in relational algebra.
A substitution ![]() from
from ![]() to
to
![]() is a partial function
is a partial function
![]() . We write substitutions in postfix notation: For a triple
pattern
. We write substitutions in postfix notation: For a triple
pattern ![]() we denote
by
we denote
by ![]() the triple
the triple
![]() obtained by applying the substitution to all variables in
obtained by applying the substitution to all variables in
![]() . The domain of
. The domain of
![]() ,
,
![]() , is the
subset of
, is the
subset of ![]() where
where ![]() is defined. For a
substitution
is defined. For a
substitution ![]() and a set
of variables
and a set
of variables
![]() we define
the substitution
we define
the substitution ![]() with domain
with domain ![]() as follows:
as follows:
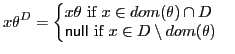
Let ![]() and
and ![]() be
substitutions, then
be
substitutions, then
![]() is
the substitution obtained as follows:
is
the substitution obtained as follows:

Now, as opposed to [16], we define three notions of compatibility between substitutions:
Analogously to [16] we define join,
union, difference, and outer join between two sets of
substitutions ![]() and
and
![]() over domains
over domains
![]() and
and ![]() , respectively, all
except union parameterized by
, respectively, all
except union parameterized by
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
The semantics of a graph pattern ![]() over dataset
over dataset
![]() , can now be
defined recursively by the evaluation function returning sets of
substitutions.
, can now be
defined recursively by the evaluation function returning sets of
substitutions.
Take for instance,
![]() and
and
![]() AND
AND
![]() . When viewing each solution
set as a relational table with variables denoting attribute
names, we can write:
. When viewing each solution
set as a relational table with variables denoting attribute
names, we can write:
| ?X | ?Name |
|
|
"Bob" |
| alice.org#me | "Alice" |
|
|
"Bob" |
| ?X | ?Friend |
|
|
|
| alice.org#me |
|
| ?X | ?Name | ?Friend |
|
|
"Bob" |
|
| alice.org#me | "Alice" |
|
Differences between the three semantics appear when joining over null-bound variables, as shown in the next example.
Again, we consider the tabular view of the resulting join: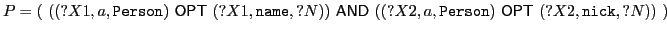
| ?X1 | ?N |
|
|
"Bob" |
|
|
null |
|
|
"Bob" |
| alice.org#me | "Alice" |
| ?X2 | ?N |
|
|
null |
|
|
"Alice" |
|
|
"Bobby" |
| alice.org#me | null |
Now, let us see what happens when we evaluate the join
![]() with respect
to the different semantics. The following result table lists in
the last column which tuples belong to the result of b-, c- and
s-join, respectively.
with respect
to the different semantics. The following result table lists in
the last column which tuples belong to the result of b-, c- and
s-join, respectively.
| ?X1 | ?N | X2 | |
|
|
"Bob" |
|
b |
|
|
"Bob" | alice.org#me | b |
|
|
null |
|
b,c |
|
|
"Alice" |
|
b |
|
|
"Bobby" |
|
b |
|
|
null | alice.org#me | b,c |
|
|
"Bob" |
|
b |
|
|
"Bob" | alice.org#me | b |
| alice.org#me | "Alice" |
|
b |
| alice.org#me | "Alice" |
|
b,c,s |
| alice.org#me | "Alice" | alice.org#me | b |
Compared to how joins over incomplete relations are treated in common relational database systems, the s-joining semantics might be considered the intuitive behavior. Another interesting divergence (which would rather suggest to adopt the c-joining semantics) shows up when we consider a simple idempotent join.
![]()
Clearly, this pattern, has the solution set
![]()
under all three semantics. Surprisingly,
![]() has different solution
sets for the different semantics. First,
has different solution
sets for the different semantics. First,
![]() , but
, but
![]() , since null values are
not compatible under the s-joining semantics. Finally,
, since null values are
not compatible under the s-joining semantics. Finally,
![]()
As shown by this example, under the reasonable assumption,
that the join operator is idempotent, i.e.,
![]() ,
only the c-joining semantics behaves correctly.
,
only the c-joining semantics behaves correctly.
![]()
Only
![]() contains
the expected solution
contains
the expected solution
![]() for the bNode
for the bNode
![]() .
.
All three semantics may be considered as variations of the original definitions in [16], for which the authors proved complexity results and various desirable features, such as semantics-preserving normal form transformations and compositionality. The following proposition shows that all these results carry over to the normative b-joining semantics:
Following the definitions from the SPARQL specification and [16], the b-joining semantics is the only admissible definition. There are still advantages for gradually defining alternatives towards traditional treatment of joins involving null s. On the one hand, as we have seen in the examples above, the brave view on joining unbound variables might have partly surprising results, on the other hand, as we will see, the c- and s-joining semantics allow for a more efficient implementation in terms of Datalog rules.
Let us now take a closer look on some properties of the three defined semantics.
The following proposition summarizes equivalences which hold for all three semantics, showing some interesting additions to the results of Pérez et al.
(1) AND, UNION are associative and
commutative. (b,c,s)
(2)
![]() . (b)
. (b)
(3)
![]() . (b)
. (b)
(4)
![]() . (b)
. (b)
(5)
![]() . (b,c,s)
. (b,c,s)
(6) AND is idempotent, i.e.
![]() . (c)
. (c)
Ideally, we would like to identify a subclass of programs, where the three semantics coincide. Obviously, this is the case for any query involving neither UNION nor OPT operators. Pérez et al. [16] define a bigger class of programs, including ``well-behaving'' optional patterns:
Likewise, we can identify ``dangerous'' variables in graph patterns, which might cause semantic differences:
We now define solution tuples that were informally
introduced in Sec. 2. Recall that by
![]() we denote
the tuple obtained from lexicographically ordering a set of
variables in
we denote
the tuple obtained from lexicographically ordering a set of
variables in ![]() . The notion
. The notion
![]() means that,
after ordering
means that,
after ordering ![]() all variables
from a subset
all variables
from a subset
![]() are
replaced by null.
are
replaced by null.
In this paper we will use a very general form of Datalog commonly referred to as Answer Set Programming (ASP), i.e. function-free logic programming (LP) under the answer set semantics [1, 11]. ASP is widely proposed as a useful tool for various problem solving tasks in e.g. Knowledge Representation and Deductive databases. ASP extends Datalog with useful features such as negation as failure, disjunction in rule heads, aggregates [9], external predicates[8], etc. 8
Let ![]() ,
, ![]() ,
, ![]() ,
, ![]() be sets of
predicate, constant, variable symbols, and external predicate
names, respectively. Note that we assume all these sets except
be sets of
predicate, constant, variable symbols, and external predicate
names, respectively. Note that we assume all these sets except
![]() and
and ![]() (which may
overlap), to be disjoint. In accordance with common notation in
LP and the notation for external predicates from [7] we will in the
following assume that
(which may
overlap), to be disjoint. In accordance with common notation in
LP and the notation for external predicates from [7] we will in the
following assume that ![]() and
and
![]() comprise sets of
numeric constants, string constants beginning with a lower case
letter, or '"' quoted strings, and strings of the form
comprise sets of
numeric constants, string constants beginning with a lower case
letter, or '"' quoted strings, and strings of the form
![]() quoted-string
quoted-string![]()
^^![]() IRI
IRI![]() ,
,
![]() quoted-string
quoted-string
![]() valid-lang-tag
valid-lang-tag![]() ,
,
![]() is the set of string
constants beginning with an upper case letter. Given
is the set of string
constants beginning with an upper case letter. Given
![]() an
atom is defined as
an
atom is defined as
![]() ,
where
,
where ![]() is called the arity of
is called the arity of
![]() and
and
![]() .
.
Moreover, we define a fixed set of external predicates
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() All external predicates
have a fixed semantics and fixed arities, distinguishing
input and output terms. The atoms
All external predicates
have a fixed semantics and fixed arities, distinguishing
input and output terms. The atoms
![]() ,
,
![]() ,
,
![]() test
the input term
test
the input term
![]() (in
square brackets) for being valid string representations of Blank
nodes, IRI References or RDF literals, returning an output value
(in
square brackets) for being valid string representations of Blank
nodes, IRI References or RDF literals, returning an output value
![]() ,
representing truth, falsity or an error, following the semantics
defined in [18, Sec.
11.3]. For the
,
representing truth, falsity or an error, following the semantics
defined in [18, Sec.
11.3]. For the ![]() predicate we
write atoms as
predicate we
write atoms as
![]() to denote
that
to denote
that
![]() is
an input term, whereas
is
an input term, whereas
![]() are output terms which may be bound by the external predicate.
The external atom
are output terms which may be bound by the external predicate.
The external atom
![]() is true if
is true if
![]() is an RDF
triple entailed by the RDF graph which is accessibly at
IRI
is an RDF
triple entailed by the RDF graph which is accessibly at
IRI ![]() . For the moment, we
consider simple RDF entailment [13] only. Finally, we write
comparison atoms '
. For the moment, we
consider simple RDF entailment [13] only. Finally, we write
comparison atoms '![]() '
and '
'
and '
![]() ' in infix notation
with
' in infix notation
with
![]() and the obvious semantics of (lexicographic or numeric)
(in)equality. Here, for
and the obvious semantics of (lexicographic or numeric)
(in)equality. Here, for ![]() either
either ![]() or
or ![]() is an output term,
but at least one is an input term, and for
is an output term,
but at least one is an input term, and for
![]() both
both ![]() and
and ![]() are
input terms.
are
input terms.
The notion of input and output terms in external atoms
described above denotes the binding pattern. More precisely, we
assume the following condition which extends the standard notion
of safety (cf. [21])
in Datalog with negation: Each variable appearing in a rule must
appear in ![]() in an atom or
as an output term of an external atom.
in an atom or
as an output term of an external atom.
An interpretation relative to ![]() is any subset
is any subset
![]() containing only atoms. We
say that
containing only atoms. We
say that
![]() is a
model of atom
is a
model of atom
![]() , denoted
, denoted
![]() , if
, if
![]() . With
every external predicate name
. With
every external predicate name
![]() with arity
with arity
![]() we associate an
we associate an
![]() -ary Boolean
function
-ary Boolean
function ![]() (called
oracle function) assigning each tuple
(called
oracle function) assigning each tuple
![]() either 0 or
either 0 or ![]() . 11We say that
. 11We say that
![]() is a model of a
ground external atom
is a model of a
ground external atom
![]()
![]() , denoted
, denoted
![]() ,
iff
,
iff
![]() .
.
The semantics we use here generalizes the answer-set semantics [11]12, and is defined using the FLP-reduct [9], which is more elegant than the traditional GL-reduct [11] of stable model semantics and ensures minimality of answer sets also in presence of external atoms.
Let ![]() be a ground rule. We
define (i)
be a ground rule. We
define (i)
![]() iff
iff
![]() for all
for all
![]() and
and
![]() for all
for all
![]() , and (ii)
, and (ii)
![]() iff
iff
![]() whenever
whenever
![]() . We say that
. We say that
![]() is a
model of a program
is a
model of a program ![]() , denoted
, denoted
![]() , iff
, iff
![]() for all
for all
![]() .
.
The FLP-reduct [9] of ![]() with respect to
with respect to
![]() , denoted
, denoted
![]() , is
the set of all
, is
the set of all
![]() such that
such that
![]() .
.
![]() is an
answer set of
is an
answer set of ![]() iff
iff
![]() is a minimal
model of
is a minimal
model of
![]() .
.
By ![]() we mean the
set of rules resulting from disassembling complex FILTER
expressions (involving '
we mean the
set of rules resulting from disassembling complex FILTER
expressions (involving '![]() ','
','![]() ','
','![]() ') according to the
rewriting defined by Lloyd and Topor [15] where we have to obey
the semantics for errors, following Definition 2. In a nutshell, the rewriting
') according to the
rewriting defined by Lloyd and Topor [15] where we have to obey
the semantics for errors, following Definition 2. In a nutshell, the rewriting
![]() proceeds as follows: Complex filters involving
proceeds as follows: Complex filters involving ![]() are transformed into
negation normal form. Conjunctions of filter expressions are
simply disassembled to conjunctions of body literals,
disjunctions are handled by splitting the respective rule for
both alternatives in the standard way. The resulting rules
involve possibly negated atomic filter expressions in the bodies.
Here,
are transformed into
negation normal form. Conjunctions of filter expressions are
simply disassembled to conjunctions of body literals,
disjunctions are handled by splitting the respective rule for
both alternatives in the standard way. The resulting rules
involve possibly negated atomic filter expressions in the bodies.
Here, ![]() is translated
to
is translated
to
![]() ,
,
![]() to
to
![]() .
.
![]() ,
, ![]() ,
,
![]() and their
negated forms are replaced by their corresponding external atoms
(see Sec. 3)
and their
negated forms are replaced by their corresponding external atoms
(see Sec. 3)
![]() or
or
![]() , etc.,
respectively.
, etc.,
respectively.
The resulting program
![]() implements the c-joining
semantics in the following sense:
implements the c-joining
semantics in the following sense:
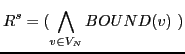
Step 1. We rename each variable ![]() in the respective rule bodies to
in the respective rule bodies to
![]() or
or ![]() , respectively, in
order to disambiguate the occurrences originally from sub-pattern
, respectively, in
order to disambiguate the occurrences originally from sub-pattern
![]() or
or ![]() , respectively. That
is, for each rule (2) or (6'), we rewrite the body to:
, respectively. That
is, for each rule (2) or (6'), we rewrite the body to:
![]()
![]()
Step 2. We now add the following FILTER
expressions ![]() and
and
![]() ,
respectively, to the resulting rule bodies which ``emulate'' the
relaxed b-compatibility:
,
respectively, to the resulting rule bodies which ``emulate'' the
relaxed b-compatibility:
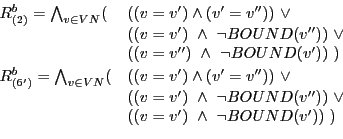
As it turns out, the embedding of SPARQL in the rules world opens a wide range of possibilities for combinations. In this section, we will first discuss some straightforward extensions of SPARQL which come practically for free with the translation to Datalog provided before. We will then discuss the use of SPARQL itself as a simple RDF rules language14 which allows to combine RDF fact bases with implicitly specified further facts and discuss the semantics thereof briefly. We conclude this section with revisiting the open issue of entailment regimes covering RDFS or OWL semantics in SPARQL.
Intuitively, in the translation of CONSTRUCT we
``stored'' the new triples in a new triple outside the dataset
![]() . We can imagine a
similar construction in order to define the semantics of queries
over datasets mixing such CONSTRUCT statements with RDF
data in the same turtle file.
. We can imagine a
similar construction in order to define the semantics of queries
over datasets mixing such CONSTRUCT statements with RDF
data in the same turtle file.
Let us assume such a mixed file containing CONSTRUCT
rules and RDF triples web-accessible at IRI ![]() , and a query
, and a query
![]() , with
, with
![]() . The
semantics of a query over a dataset containing
. The
semantics of a query over a dataset containing ![]() may then be defined by
recursively adding
may then be defined by
recursively adding
![]() to
to
![]() for any CONSTRUCT query
for any CONSTRUCT query
![]() in
in
![]() plus the rules
(2) above with their head changed to
plus the rules
(2) above with their head changed to
![]() . We further need to add a rule
. We further need to add a rule
Naturally, the resulting programs possibly involve recursion, and, even worse, recursion over negation as failure. Fortunately, the general answer set semantics, which we use, can cope with this. For some important aspects on the semantics of such distributed rules and facts bases, we refer to [17], where we also outline an alternative semantics based on the well-founded semantics. A more in-depth investigation of the complexity and other semantic features of such a combination is on our agenda.
Finite rule sets which approximate the RDF(S) semantics in
terms of positive Datalog rules [17] have been
implemented in systems like TRIPLE15 or JENA16.
Similarly, fragments and extensions of OWL [12,3,14] definable in terms of
Datalog rule bases have been proposed in the literature. Such
rule bases can be parametrically combined with our translations,
implementing what one might call RDFS![]() or OWL
or OWL![]() entailment at least. It remains to be seen whether the SPARQL
working group will define such reduced entailment regimes.
entailment at least. It remains to be seen whether the SPARQL
working group will define such reduced entailment regimes.
More complex issues arise when combining a nonmonotonic query language like SPARQL with ontologies in OWL. An embedding of SPARQL into a nonmonotonic rules language might provide valuable insights here, since it opens up a whole body of work done on combinations of such languages with ontologies [7,19].
A prototype of the presented translation has been implemented on top of the dlvhex system, a flexible framework for developing extensions for the declarative Logic Programming Engine DLV17. The prototype is available as a plugin at http://con.fusion.at/dlvhex/. The web-page also provides an online interface for evaluation, where the reader can check translation results for various example queries, which we had to omit here for space reasons. We currently implemented the c-joining and b-joining semantics and we plan to gradually extend the prototype towards the features mentioned in Sec. 5, in order to query mixed RDF+SPARQL rule and fact bases. Implementation of further extensions, such as the integration of aggregates typical for database query language, and recently defined for recursive Datalog programs in a declarative way compatible with the answer set semantics [9], are on our agenda. We are currently not aware of any other engine implementing the full semantics defined in [16].