1 Introduction
Why are cyber-communities important?. Searching for
social structures in the World Wide Web has emerged as one of
the foremost research problems related to the breathtaking
expansion of the World Wide Web. Thus there is a keen academic
as well as industrial interest in developing efficient
algorithms for collecting, storing and analyzing the pattern of
pages and hyper-links that form the World Wide Web, since the
pioneering work of Gibson, Kleinberg and Raghavan [19]. Nowadays many
communities of the real world that want to have a major impact
and recognition are represented in the Web. Thus the detection
of cyber-communities, i.e. set of sites and pages
sharing a common interest, improves also our knowledge of the
world in general.
Cyber-communities as dense subgraphs of the web
graph. The most popular way of defining cyber-communities
is based on the interpretation of WWW hyperlinks as
social links [10]. For
example, the web page of a conference contains an hyper-link to
all of its sponsors, similarly the home-page of a car lover
contains links to all famous car manufactures. In this way, the
Web is modelled by the web graph, a directed
graph in which each vertex represents a web-page and each
arc represents an hyper-link between the two corresponding
pages. Intuitively, cyber-communities correspond to dense
subgraphs of the web graph.
An open problem. Monika Henzinger in a recent survey
on algorithmic challenges in web search engines [26] remarks that the
Trawling algorithm of Kumar et al. [31] is able to
enumerate dense bipartite graphs in the order of tens of nodes
and states this open problem: ``In order to more completely
capture these cyber-communities, it would be interesting to
detect much larger bipartite subgraphs, in the order of
hundreds or thousands of nodes. They do not need to be
complete, but should be dense, i.e. they should contain at
least a constant fraction of the corresponding complete
bipartite subgraphs. Are there efficient algorithms to detect
them? And can these algorithms be implemented efficiently if
only a small part of the graph fits in main memory?
Theoretical results. From a theoretical point of
view, the dense 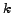 -subgraph problem, i.e. finding the densest
subgraph with
-subgraph problem, i.e. finding the densest
subgraph with 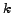 vertices in a given graph, is clearly NP-Hard (it is easy to
see by a reduction from the max-clique problem). Some
approximation algorithms with a non constant approximation
factor can be found in the literature for example in [24,14,13], none of which seem
to be of practical applicability. Studies about the inherent
complexity of the problem of obtaining a constant factor
approximation algorithm are reported in [25] and [12].
vertices in a given graph, is clearly NP-Hard (it is easy to
see by a reduction from the max-clique problem). Some
approximation algorithms with a non constant approximation
factor can be found in the literature for example in [24,14,13], none of which seem
to be of practical applicability. Studies about the inherent
complexity of the problem of obtaining a constant factor
approximation algorithm are reported in [25] and [12].
Some heuristic methods. In the literature there are a
few heuristic methods to extract communities from the web (or
from large graphs in general). The most important and ground
breaking algorithm is due to Kumar et al. in [31] where the authors
aim at enumerating complete bipartite subgraphs with very few
vertices, then extend them to dense bipartite
subgraphs by using local searches (based on the HITS
ranking algorithm). The technique in [31] is aimed at
detecting small complete bipartite communities, of the order of
ten vertices, while the subsequent community expansion guided
by the hub and authority scores of the HITS algorithm
(regardless of further density considerations). In [16] Flake, Lawrence,
Giles and Coetzee use the notion of maximum flow to extract
communities, but they are also limited to communities for which
an initial seed node is available. In [20] Gibson, Kumar and
Tomkins use a new sampling method (shingling) based on the
notion of min-wise independent permutations, introduced in [7], to evaluate the
similarity of neighborhoods of vertices and then extract very
large and very dense subgraphs of the web-host graph. This
technique is specifically aimed to detecting very large and
dense subgraphs, in a graph, like the web-host-graph of quite
large average degree. The authors in [20, Section 4.2] remark
that (with a reasonable set of parameters) the shingling method
is effective for dense subgraphs of over 50 nodes but breaks
down below 24 nodes. Thus there is room for improvements via
alternative approaches.
Our contribution. In this paper we propose two new
simple characterization of dense subgraphs. From these
characterization we derive a new heuristic, which is based on a
two-step filtering approach. In the first filtering step we
estimate efficiently the average degree and the similarity of
neighbor sets of vertices of a candidate community. This
initial filtering is very efficient since it is based only on
degree-counting. The second filtering step is based on an
iterative refinement of the candidate community aimed at
removing small degree vertices (relative to the target average
density), and thus increasing the average degree of the
remaining ``core`` community. We test our algorithm on very
large snapshots of the web graph (both for the global web-graph
and for some large national domains) and we give experimental
evidence the effectiveness of the method. We have coupled the
community extraction algorithm with a clustering tool that
groups the communities found into homogeneous groups by topic
and provide a useful user interface for exploring the community
data. The user interface of the Community Watch system
is publicly available at http://comwatch.iit.cnr.it.
To the best of our knowledge this is the first publicly
available tool to visualize cyber-communities.
Target size. In our method the user supplies a target
threshold 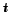 and the
algorithm lists all the communities found with average degree
at least
and the
algorithm lists all the communities found with average degree
at least 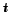 . Naturally the
lower the
. Naturally the
lower the 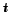 -value the more
communities will be found and the slower the method. In our
experiments our method is still effective for values of
-value the more
communities will be found and the slower the method. In our
experiments our method is still effective for values of 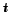 quite close to
the average degree of the web-graphs (say within a factor 2),
and communities of a few tens of nodes. Our heuristic is
particularly efficient for detecting communities of large and
medium size, while the method in [31] is explicitly
targeted towards communities with a small complete bipartite
core-set.
quite close to
the average degree of the web-graphs (say within a factor 2),
and communities of a few tens of nodes. Our heuristic is
particularly efficient for detecting communities of large and
medium size, while the method in [31] is explicitly
targeted towards communities with a small complete bipartite
core-set.
Final applications. The detection of dense subgraphs
of the web-graph might serve as a stepping stone towards
achieving several broader goals. One possible goal is to
improve the performance of critical tools in the WWW
infrastructure such as crawlers, indexing and ranking
components of search engines. In this case often dense
subgraphs are associated with negative phenomena such as the
Tightly Knit Community (TKC) effect [34],
link-farm spamming [23], and data
duplication (mirroring) [2]. In
this paper, following [33] we
place instead the accent on the ``positive`` aspect of
cyber-communities: our intent at the moment is to provide an
exploratory tool capable of extracting a synthetic description
of the current status and current trends in the social
structure of the WWW.
Visualization of the Communities. Given a single
dense community it is easy by manual inspection to gain some
hint as to its general area of interest and purpose, however
gaining insight on hundreds (or thousands) of communities can
become a tiresome task, therefore we have coupled our
dense-subgraph extraction algorithm with a visualization tool
that helps in the exploratory approach. This tool is based on
the efficient clustering/labelling system described in detail
in [17][18]. In nutshell
from each community, using standard IR techniques, we extract a
vector of representative words with weights related to the
words frequencies (word-vector). A clustering algorithm is
applied to the word-vectors and we obtain groups of communities
that are homogeneous by topic, moreover a list of
representative keywords for each cluster is generated so to
guide the user to assess the intrinsic topic of each cluster of
communities.
Mirrors and Link-farms. Information retrieval on the
WWW is complicated by the phenomenon of ``data replication``
(mirroring) and several forms of spamming (e.g. link-farms).
For mirrors, off-line detection of such structures using the
techniques in [2] implies
pairwise comparisons of all (or most if some heuristic
filtering is used) pairs of web-sites, which is an expensive
computations. Link-farm detection implies technique borderline
with those used for community detection. In our context,
however, efficiency and effectiveness of the community
detection algorithm are not really impaired by such borderline
phenomena. For this reason we do not attempt to filter out
these phenomena before applying our algorithms. Instead we
envision these steps (mirror detection and link-farm detection)
as a post-processing phase in our Community Watch
system. In particular since we perform efficiently both the
community detection and community clustering we can apply
mirror and link-farm detection separately and independently in
each cluster thus retaining the overall system scalability.
2 Previous work
Given the hypertext nature of the WWW one can approach the
problem of finding cyber-communities by using as main source
the textual content of the web pages, the hyperlinks structure,
or both. Among the methods for finding group of coherent pages
based only on text content we can mention [8]. Recommendation
systems usually collect information on social networks from a
variety of sources (not only link structure) (e.g. [29]).
Problems of a similar nature appears in the areas of social
network analysis, citation analysis and bibliometrics, where
however, given the relatively smaller data sets involved
(relative to the WWW), efficiency is often not a critical issue
[35].
Since the pioneering work [19] the prevailing
trend in the Computer Science community is to use mainly the
link-structure as basis of the computation. Previous literature
on the problem of finding cyber-communities using link-based
analysis in the web-graph can be broadly split into two large
groups. In the first group are methods that need an initial
seed of a community to start the process of community
identification. Assuming the availability of a seed for a
possible community naturally directs the computational effort
in the region of the web-graph closest to the seed and suggests
the use of sophisticated but computational intensive
techniques, usually based of max-flow/min-cut approaches. In
this category we can list the work of [19,15,16,27,28]. The second group
of algorithms does not assume any seed and aims at finding all
(or most) of the communities by exploring the whole web graph.
In this category falls the work of [31,30,36,32,20].
Certain particular artifacts in the WWW called ``link farms``
whose purpose is to bias search-engines pagerank-type ranking
algorithms are a very particular type of ``artificial``
cyber-community that is traced using techniques bordering with
those used to find dense subgraphs in general. See for example
[37,3].
Abello et al. [1]
propose a method based on local searches with random restarts
to escape local minima, which is quite computational intensive.
A graph representing point to point telecommunications with 53
M nodes and 170M edges is used as input. The equipment used is
a multiprocessor machine of 10 200MHz processors and total 6GB
RAM memory. A timing result of roughly 36 hours is reported in
[1] for an
experiment handling a graph obtained by removing all nodes of
degree larger than 30, thus, in effect, operating on a reduced
graph of 9K nodes and 320K edges. Even discounting for the
difference in equipment we feel that the method in [1] would not scale well
to searching for medium-density and medium-size communities in
graphs as large as those we are able to handle (up to 20M nodes
and 180M edges after cleaning). Girvan and Newman [21] define a notion of
local density based on counting the number of shortest paths in
a graph sharing a given edge. This notion, though powerful,
entails algorithm that do not scale well to the size of the
web-graph. Spectral methods described in [9] also lack
scalability (i.e. in [9] the method is
applied to graphs from psychological experiments with 10K nodes
and 70K edges).
A system similar in spirit to that proposed in this paper is
Campfire described in [33] which
is based on the Trawling algorithm for finding the dense core,
on HITS for community expansion and on an indexing structure of
community keywords that can be queried by the user. Our system
is different from Campfire first of all in the algorithms used
to detect communities but also in the final user interface: we
provide a clustering/labelling interface that is suitable to
giving a global view of the available data.
3 Preliminaries
A directed graph 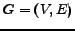 consists of a set
consists of a set 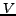 of
vertices and a set
of
vertices and a set 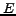 of arcs, where an arc is an ordered pair of
vertices. The web graph is the directed graph
representing the Web: vertices are pages and arcs are
hyperlinks.
of arcs, where an arc is an ordered pair of
vertices. The web graph is the directed graph
representing the Web: vertices are pages and arcs are
hyperlinks.
Let 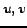 be any
vertices of a directed graph
be any
vertices of a directed graph 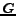 , if there exists an arc
, if there exists an arc  , then
, then  is an
outlink of
is an
outlink of 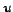 , and
an inlink of
, and
an inlink of 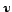 .
Moreover,
.
Moreover, 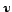 is called a
successor of
is called a
successor of 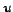 , and
, and
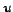 a
predecessor of
a
predecessor of 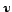 . For every vertex
. For every vertex 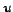 ,
,
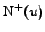 denotes the set of its successors, and
denotes the set of its successors, and
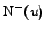 the set of its predecessors. Then, the outdegree and the
indegree of
the set of its predecessors. Then, the outdegree and the
indegree of 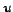 are
respectively
are
respectively
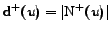 and
and
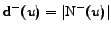 . Let
. Let 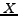 by any subset of
by any subset of
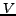 , the successors
and the predecessors of
, the successors
and the predecessors of 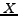 are respectively defined by:
are respectively defined by:
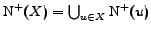 and
and
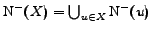 .
Observe that
.
Observe that
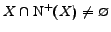 is
possible.
is
possible.
A graph 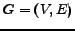 is called a complete bipartite graph, if
is called a complete bipartite graph, if 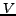 can be
partitioned into two disjoint subsets
can be
partitioned into two disjoint subsets 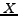 and
and 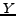 , such that, for
every vertex
, such that, for
every vertex 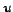 of
of
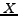 , the set of
successors of
, the set of
successors of 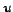 is
exactly
is
exactly 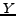 , i.e.,
, i.e.,
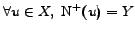 . Consequently for
every node
. Consequently for
every node 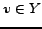 its predecessor set is
its predecessor set is 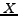 . Finally, let
. Finally, let
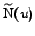 be the set of vertices
that share at least one successor with
be the set of vertices
that share at least one successor with 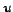 :
:
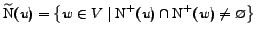 .
.
Two more useful definitions. Define for sets 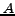 and
and 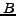 the relation
the relation
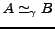 when
when
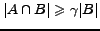 ,
for a constant
,
for a constant  .
Define for positive numbers
.
Define for positive numbers 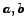 the relation
the relation 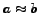 when
when
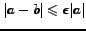 , for
a constant
, for
a constant 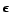 . When the constant is not important for the
discussion or it can be inferred from the context the subscript
is omitted.
. When the constant is not important for the
discussion or it can be inferred from the context the subscript
is omitted.
The basic argument linking the (informal) notion of web
communities and the (formal) notion of dense subgraphs is
developed and justified in [31]. It is summarized
in [31] as follows:
``Web communities are characterized by dense directed bipartite
subgraph". Without entering in a formal definition of density
in [31] it is
stated the hypothesis that:``A random large enough and dense
enough bipartite subgraph of the Web almost surely has a core",
(i.e. a complete bipartite sub-graph of size 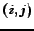 for some
small integer values,
for some
small integer values, 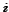 and
and
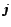 ). A standard
definition of
). A standard
definition of  -density, as used for example in [20], is as follows: a
-density, as used for example in [20], is as follows: a
 -dense
bipartite subgraph of a graph
-dense
bipartite subgraph of a graph 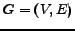 is a disjoint pair of sets of vertices,
is a disjoint pair of sets of vertices,
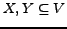 such that
such that
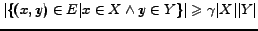 , for a real parameter
, for a real parameter
![$\gamma \in [0..1]$](www015-pellegrini-img46.png) .
Note that
.
Note that 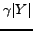 is also a lower bound to the average out-degree of a node in
is also a lower bound to the average out-degree of a node in
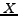 . Similarly a
dense quasi-clique is a subset
. Similarly a
dense quasi-clique is a subset 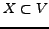 such that
such that
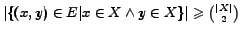 , for a real parameter
, for a real parameter
![$\gamma \in [0..1]$](www015-pellegrini-img46.png) ,
as in [1,14]. This notion of a
core of a dense subgraph in [31] is consistent with
the notion of
,
as in [1,14]. This notion of a
core of a dense subgraph in [31] is consistent with
the notion of  -density for values of
-density for values of  large
enough, where the notion of ``almost surely``,
large
enough, where the notion of ``almost surely``,  -core,
``large enough", ``dense enough", must be interpreted as a
function of
-core,
``large enough", ``dense enough", must be interpreted as a
function of  .
Our formulation unifies the notion of a
.
Our formulation unifies the notion of a  -dense
bipartite subgraph and a
-dense
bipartite subgraph and a  -clique as a pair of not necessarily disjoint
sets of vertices,
-clique as a pair of not necessarily disjoint
sets of vertices,
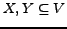 such that
such that
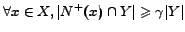 and
and
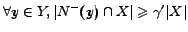 . For two constants
. For two constants  and
and 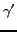 . Our
definition implies that in [20], and conversely,
any
. Our
definition implies that in [20], and conversely,
any  -dense
subgraph following [20] contains a
-dense
subgraph following [20] contains a  -dense
subgraph in our definition1.
-dense
subgraph in our definition1.
Thus a community in the web is defined by two sets of pages,
the set of the 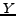 centers of the community, i.e. pages sharing a common
topic, and the set
centers of the community, i.e. pages sharing a common
topic, and the set 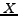 of
the fans, i.e., pages that are interested in the topic.
Typically, every fan contains a link to most of the centers, at
the same time, there are few links among centers (often for
commercial reasons) and among fans (fans may not know each
other).
of
the fans, i.e., pages that are interested in the topic.
Typically, every fan contains a link to most of the centers, at
the same time, there are few links among centers (often for
commercial reasons) and among fans (fans may not know each
other).
4 Heuristic for large dense subgraphs extraction
The definition of  -dense subgraph can be used to test
if a pair of sets
-dense subgraph can be used to test
if a pair of sets
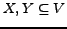 is
a
is
a  -dense
subgraph (both bipartite and clique). However it cannot be used
to find efficiently a
-dense
subgraph (both bipartite and clique). However it cannot be used
to find efficiently a  -dense subgraph
-dense subgraph 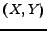 embedded in
embedded in 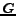 . In the following of this section we discuss a
sequence of properties and then we will proceed by
relaxing them up to the point of having properties
that can be computed directly on the input graph
. In the following of this section we discuss a
sequence of properties and then we will proceed by
relaxing them up to the point of having properties
that can be computed directly on the input graph 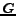 . These
properties will hold exactly (with equality) for an
isolated complete bipartite graph (and clique), will
hold approximately for an isolated
. These
properties will hold exactly (with equality) for an
isolated complete bipartite graph (and clique), will
hold approximately for an isolated  -dense
graph, where the measure of approximation will be related to
the parameter
-dense
graph, where the measure of approximation will be related to
the parameter  .
However at the end we need a the final relaxation step in which
we will consider the subgraphs as embedded in
.
However at the end we need a the final relaxation step in which
we will consider the subgraphs as embedded in 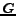 .
.
First of all, let us give an initial intuition of the reason
why our heuristic might work. Let 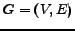 be a sparse directed graph, and let
be a sparse directed graph, and let 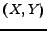 be a
be a  -dense
subgraph within
-dense
subgraph within 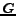 .
Then, let
.
Then, let 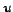 be any vertex of
be any vertex of
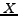 . Since
. Since  is a
is a  -dense
subgraph by definition we have
-dense
subgraph by definition we have
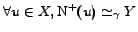 ,
and symmetrically
,
and symmetrically
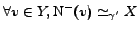 .
For values
.
For values 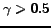 the pigeon hole principle ensures
that any two nodes
the pigeon hole principle ensures
that any two nodes  and
and
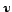 of
of 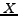 always share a
successor in
always share a
successor in 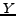 , thus
, thus
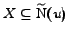 , and, if every
vertex of
, and, if every
vertex of 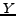 has at least a
predecessor in
has at least a
predecessor in 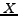 , also
, also
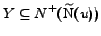 . The main
idea now is to estimate quickly, for every vertex
. The main
idea now is to estimate quickly, for every vertex 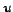 of
of 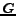 , the degree of
similarity of
, the degree of
similarity of
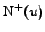 and
and
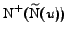 . In the case
of an isolated complete bipartite graph
. In the case
of an isolated complete bipartite graph
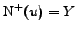 ,
and
,
and
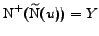 . For an
isolated
. For an
isolated  -dense
bipartite graph, we have
-dense
bipartite graph, we have
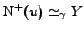 and
and
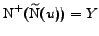 . The
conjecture is that when the
. The
conjecture is that when the  -dense bipartite graph is a subgraph of
-dense bipartite graph is a subgraph of 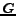 , and thus we
have the weaker relationship
, and thus we
have the weaker relationship
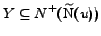 , the
excess
, the
excess
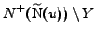 is small
compared to
is small
compared to 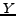 so to
make the comparison of the two sets still significant for
detecting the presence of a dense subgraph.
so to
make the comparison of the two sets still significant for
detecting the presence of a dense subgraph.
To gain in efficiency, instead of evaluating the similarity
of successor set, we will estimate the similarity of
out-degrees by counting. In a complete bipartite graph 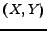 , we have
that
, we have
that
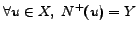 , therefore,
, therefore,
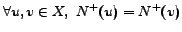 . The set of
vertices sharing a successor with
. The set of
vertices sharing a successor with 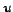 is
is
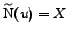 , and moreover
, and moreover
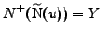 . Passing from
relations among sets to relations among cardinalities we have
that:
. Passing from
relations among sets to relations among cardinalities we have
that:
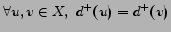 , and the degree of
any node coincide with the average out-degree:
, and the degree of
any node coincide with the average out-degree:
In a  -dense
bipartite graph, we still have
-dense
bipartite graph, we still have
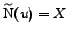 but now,
but now,
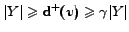 for every
for every 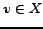 . Thus we can conclude that
. Thus we can conclude that
For
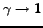 the difference tends to zero.
Finally assuming that for a
the difference tends to zero.
Finally assuming that for a  -dense bipartite subgraph of
-dense bipartite subgraph of  the excesses
the excesses
 and
and
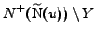 give a
small contribution, we can still use the above test as evidence
of the presence of a dense sub-graph. At this point we pause,
we state our first criterion and we subject it to criticism in
order to improve it.
give a
small contribution, we can still use the above test as evidence
of the presence of a dense sub-graph. At this point we pause,
we state our first criterion and we subject it to criticism in
order to improve it.
Criterion 1
If
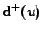 and
and
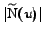 are big enough
and
then
are big enough
and
then
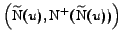 might contain a community.
might contain a community.
Unfortunately, this criterion 1
cannot be used yet in this form. One reason is that computing
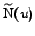 for every vertex
for every vertex 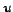 of big enough
outdegree in the web graph
of big enough
outdegree in the web graph 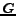 is not scalable. Moreover, the criterion is not
robust enough w.r.t. noise from the graph. Assume that the
situation depicted in figure 1
occurs:
is not scalable. Moreover, the criterion is not
robust enough w.r.t. noise from the graph. Assume that the
situation depicted in figure 1
occurs:  ,
, 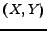 induces a
complete bipartite graph with
induces a
complete bipartite graph with 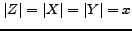 , and each
vertex of
, and each
vertex of 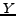 has one more
predecessor of degree
has one more
predecessor of degree 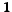 in
in 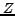 .
Then,
.
Then,
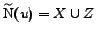 , so
, so
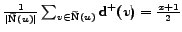 that is far from
that is far from
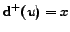 ,
so
,
so 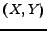 will not be
detected.
will not be
detected.
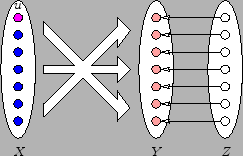
Figure 1: A complete bipartite subgraph
with 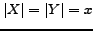 , and some
``noise``.
, and some
``noise``.
Because of the shortcomings of Criterion 1 we describe a second criterion that is
more complex to derive but computationally more effective and
robust. As before we will start with the case of the isolated
complete bipartite graph. Consider a node  , clearly
, clearly
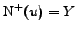 ,
and
,
and
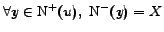 ,
thus
,
thus
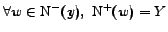 .
Turning to the cardinalities: for a node
.
Turning to the cardinalities: for a node 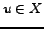 ,
,
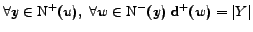 . Thus also the average value of all out-degrees for nodes in
. Thus also the average value of all out-degrees for nodes in
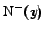 is
is
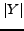 . In
formulae: given
. In
formulae: given 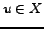 ,
,
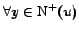 ,
,
Next we average over all
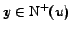 by obtaining the following
equation: given
by obtaining the following
equation: given 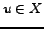 ,
,
Finally since
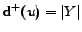 we have the
equality:
we have the
equality:
Next we see how to transform the above equality for isolated
 -dense
graphs. Consider a node
-dense
graphs. Consider a node 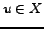 , now
, now
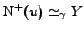 , and for a node
, and for a node
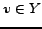 ,
,
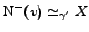 . Thus we get the
bounds:
. Thus we get the
bounds:
Thus the ratio of the two quantities is in the range
![$[\frac{\vert Y\vert}{\gamma \gamma'},\vert Y\vert\gamma^2\gamma']$](www015-pellegrini-img102.png) . On the other hand
. On the other hand
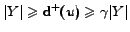 . Therefore the difference of the two terms is bounded by
. Therefore the difference of the two terms is bounded by
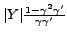 ,
which is bounded by
,
which is bounded by
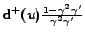 . Again for
. Again for
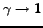 and
and
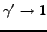 the difference tends to
zero.
the difference tends to
zero.
Thus in an approximate sense the relationship is preserved
for isolated  -dense bipartite graphs. Clearly now we will
make a further relaxation by considering the sets
-dense bipartite graphs. Clearly now we will
make a further relaxation by considering the sets
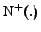 and
and
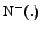 as referred to the overall graph
as referred to the overall graph 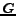 , instead of just the isolated pair
, instead of just the isolated pair 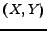 .
.
Criterion 2
If
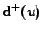 and
and
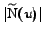 are big enough
and
then
are big enough
and
then
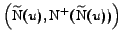 might contain a community.
might contain a community.
There are several advantages in using Criterion 2. The first advantage is that the
relevant summations are defined over sets
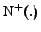 and
and
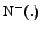 that are encoded directly in the graphs
that are encoded directly in the graphs 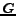 and
and 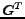 . We will
compute
. We will
compute
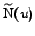 in the second phase only
for vertices that are likely to belong to a community. The
second advantage is that the result of the inner summation can
be pre-computed stored and reused. We just need to store two
tables of size
in the second phase only
for vertices that are likely to belong to a community. The
second advantage is that the result of the inner summation can
be pre-computed stored and reused. We just need to store two
tables of size 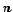 (
(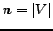 ),
one containing the values of
),
one containing the values of
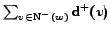 , the other
containing the indegrees. Thirdly, the criterion 2 is much more robust than criterion 1 to noise, since the outdegree of every
vertex of
, the other
containing the indegrees. Thirdly, the criterion 2 is much more robust than criterion 1 to noise, since the outdegree of every
vertex of 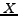 is counted many
times. For example, in the situation depicted in figure 1, we obtain the following result:
is counted many
times. For example, in the situation depicted in figure 1, we obtain the following result:
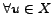 and
and
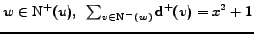 .
.
Thus,
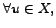
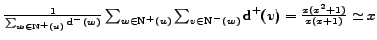 .
.
Finally, let 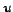 be a
vertex that satisfies the criterion 2,
we construct explicitly the two sets
be a
vertex that satisfies the criterion 2,
we construct explicitly the two sets
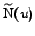 and
and
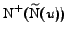 . Then, we
extract the community
. Then, we
extract the community 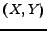 contained in
contained in
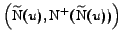 thanks to an iterative loop in which we remove from
thanks to an iterative loop in which we remove from
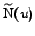 all vertices
all vertices 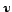 for which
for which
 is small, and we remove from
is small, and we remove from
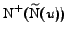 all vertices
all vertices
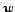 for which
for which
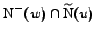 is
small.
is
small.
In figures 2 and 3 we give the pseudo-code for our
heuristic. Algorithm
 detects
vertices that satisfy the filtering formula of criterion 2, then function
detects
vertices that satisfy the filtering formula of criterion 2, then function
 computes
computes
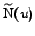 and
and
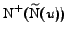 and extracts
the community of which
and extracts
the community of which 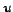 is a fan. This two algorithms are a
straightforward application of the formula in the criterion 2.
is a fan. This two algorithms are a
straightforward application of the formula in the criterion 2.
Figure:
 performs the
main filtering step.
performs the
main filtering step.
|
|
Figure:
 extracts the dense
subgraph.
extracts the dense
subgraph.
.O Function

Input: A vertex 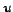 of
a directed graph of
a directed graph 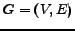 . Slackness parameter . Slackness parameter 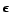
Result: A community of which 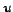 is
a fan is
a fan
begin
..
.. Initialization:
..
Iterative refinement:
..
.O repeat
..
|
Unmark potential fans of small
local outdegree;
Unmark potential centers of
small local indegree;
|
until Number of
potential fans and centers have not
changed significatively
|
..
Update global data
structures:
..
forall potential fan 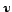 do do
..
end
|
Return (potential fans, potential
centers);
|
end
|
|
Our algorithm can capture also partially overlapping
communities. This case may happen when we have older
communities that are in the process of splitting or newly
formed communities in the process of merging. However
overlapping centers and overlapping fans are treated
differently, since the algorithm is not fully symmetric in
handling fans and centers.
Communities sharing fans. The case depicted in
Figure 4(a) is that of overlapping
fans. If the overlap 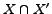 is large with respect to
is large with respect to 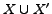 then
our algorithm will just return the union of the two communities
then
our algorithm will just return the union of the two communities
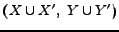 . Otherwise when the overlap
. Otherwise when the overlap
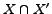 is not
large the algorithm will return two communities: either the
pairs
is not
large the algorithm will return two communities: either the
pairs 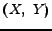 and
and
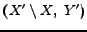 , or the pairs
, or the pairs 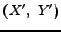 and
and
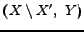 . So we will report both the
communities having their fan-sets overlapping, but the
representative fan sets will be split. The notion of
large/small overlap is a complex function of the degree
threshold and other parameters of the algorithm. In either case
we do not miss any important structure of our data.
. So we will report both the
communities having their fan-sets overlapping, but the
representative fan sets will be split. The notion of
large/small overlap is a complex function of the degree
threshold and other parameters of the algorithm. In either case
we do not miss any important structure of our data.
Communities sharing centers. Note that the behavior
is different in the case of overlapping centers. A vertex can
be a center of several communities. Thus, in the case depicted
in Figure 4(b), if the overlap
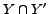 is big
with respect to
is big
with respect to 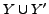 , then we will return the union of the two
communities
, then we will return the union of the two
communities
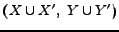 , otherwise we will return
exactly the two overlapping communities
, otherwise we will return
exactly the two overlapping communities 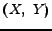 and
and 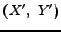 . In
either case we do not miss any important structure of our data.
Observe that the last loop of function
. In
either case we do not miss any important structure of our data.
Observe that the last loop of function
 removes logically
from the graph all arcs of the current community, but not the
vertices. Moreover, a vertex can be fan of a community and
center of several communities. In particular it can be fan and
center for the same community, so we are able to detect dense
quasi bipartite subgraphs as well as quasi cliques.
removes logically
from the graph all arcs of the current community, but not the
vertices. Moreover, a vertex can be fan of a community and
center of several communities. In particular it can be fan and
center for the same community, so we are able to detect dense
quasi bipartite subgraphs as well as quasi cliques.
![\begin{figure} \begin{center} \subfigure[Communities sharing fans]{\scalebox{... ...ox{.5}{% \input{IntersectCommunities2.pstex_t}}} \end{center} \end{figure}](www015-pellegrini-img150.png)
Figure 4: Two cases of community intersection
We perform now a semi-empirical complexity analysis in the
standard RAM model. The graph 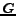 and its transpose
and its transpose 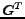 are assumed to be stored in main memory in such
a way as to be able to access a node in time
are assumed to be stored in main memory in such
a way as to be able to access a node in time  and links
incident to it in time
and links
incident to it in time  per link. We need
per link. We need  extra storage per node to store in-degree,
out-degree, a counter TabSum, and a tag bit. Algorithm
extra storage per node to store in-degree,
out-degree, a counter TabSum, and a tag bit. Algorithm
 visits each edge at
most once and performs
visits each edge at
most once and performs  operations for each edge, thus has a cost
operations for each edge, thus has a cost 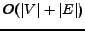 , except for the cost
of invocations of the
, except for the cost
of invocations of the
 function. Potentially the
total time cost of the invocations of
function. Potentially the
total time cost of the invocations of
 is large, however
experimentally the time cost grows only linearly with the
number of communities found. This behavior can be explained as
follows. We measured that less than 30% of the invocations do
not result in the construction of a community (see Table 5), and that the inner
refinement loop converges on average in less than 3 iterations
(see Table 4). If the number of nodes
and edges of a community found by
is large, however
experimentally the time cost grows only linearly with the
number of communities found. This behavior can be explained as
follows. We measured that less than 30% of the invocations do
not result in the construction of a community (see Table 5), and that the inner
refinement loop converges on average in less than 3 iterations
(see Table 4). If the number of nodes
and edges of a community found by
 for
for  is proportional
by a constant to the size of the bipartite sub-graph
is proportional
by a constant to the size of the bipartite sub-graph
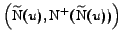 then we are allowed to charge all operations within
invocations of
then we are allowed to charge all operations within
invocations of
 to the size of the output.
Under these conditions each edge is charged on average a
constant number of operations, thus explaining the observed
overall behavior
to the size of the output.
Under these conditions each edge is charged on average a
constant number of operations, thus explaining the observed
overall behavior
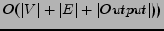 .
.
The algorithm we described, including the initial cleaning
steps, can be easily converted to work in the streaming model,
except for procedure
 that seems to require the
use of random access of data in core memory. Here we want to
estimate with a ``back of the envelope`` calculation the limits
of this approach using core memory. Andrei Broder et al. [6] in the year
2000 estimated the size of the indexable web graph at 200M
pages and 1.5G edges (thus an average degree about 7.5 links
per page, which is consistent with the average degree 8.4 of
the WebBase data of 2001). A more recent estimate by Gulli and
Signorini [22] in
2005 gives a count of 11.5G pages. The latest index-size war
ended with Google claiming an index of 25G pages. The average
degree of the webgraph has been increasing recently due to the
dynamic generation of pages with high degree, and some
measurements give a count of 40.2 The initial
cleaning phase reduces the WebBase graph by a factor 0.17 in
node count and 0.059 in the Edge count. Thus using these
coefficients the cleaned web graph might have 4.25G nodes and
59G arcs. The compression techniques in [5] for the WebBase
dataset achieves an overall performance of 3.08 bits/edge.
These coefficient applied to our cleaned web graph give a total
of 22.5Gbytes to store the graph. Storing the graph G and its
transpose we need to double the storage (although here some
saving might be achieved), thus achieving an estimate of about
45Gbytes. With current technology this amount of core memory
can certainly be provided by state of the art multiprocessors
mainframes (e.g IBM System Z9 sells in configurations ranging
from 8 to 64 GB of RAM core memory).
that seems to require the
use of random access of data in core memory. Here we want to
estimate with a ``back of the envelope`` calculation the limits
of this approach using core memory. Andrei Broder et al. [6] in the year
2000 estimated the size of the indexable web graph at 200M
pages and 1.5G edges (thus an average degree about 7.5 links
per page, which is consistent with the average degree 8.4 of
the WebBase data of 2001). A more recent estimate by Gulli and
Signorini [22] in
2005 gives a count of 11.5G pages. The latest index-size war
ended with Google claiming an index of 25G pages. The average
degree of the webgraph has been increasing recently due to the
dynamic generation of pages with high degree, and some
measurements give a count of 40.2 The initial
cleaning phase reduces the WebBase graph by a factor 0.17 in
node count and 0.059 in the Edge count. Thus using these
coefficients the cleaned web graph might have 4.25G nodes and
59G arcs. The compression techniques in [5] for the WebBase
dataset achieves an overall performance of 3.08 bits/edge.
These coefficient applied to our cleaned web graph give a total
of 22.5Gbytes to store the graph. Storing the graph G and its
transpose we need to double the storage (although here some
saving might be achieved), thus achieving an estimate of about
45Gbytes. With current technology this amount of core memory
can certainly be provided by state of the art multiprocessors
mainframes (e.g IBM System Z9 sells in configurations ranging
from 8 to 64 GB of RAM core memory).
5 Testing effectiveness
By construction algorithms
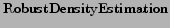 and
and
 return a list of dense
subgraph (where size and density are controlled by the
parameters
return a list of dense
subgraph (where size and density are controlled by the
parameters 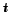 and
and 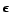 ). Using
standard terminology in Information Retrieval we can say that
full precision is guaranteed by default. In this section we
estimate the recall properties of the proposed method. This
task is complex since we have no efficient alternative method
for obtaining a guaranteed ground truth. Therefore we proceed
as follows. We add some arcs in the graph representing the
Italian domain of the year 2004, so to create new dense
subgraphs. Afterwards, we observe how many of these new
``communities'' are detected by the algorithm that is run
blindly with respect to the artificially embedded community.
The number of edges added is of the order of only 50,000 and it
is likely that the nature of a graph with 100M edges is not
affected.
). Using
standard terminology in Information Retrieval we can say that
full precision is guaranteed by default. In this section we
estimate the recall properties of the proposed method. This
task is complex since we have no efficient alternative method
for obtaining a guaranteed ground truth. Therefore we proceed
as follows. We add some arcs in the graph representing the
Italian domain of the year 2004, so to create new dense
subgraphs. Afterwards, we observe how many of these new
``communities'' are detected by the algorithm that is run
blindly with respect to the artificially embedded community.
The number of edges added is of the order of only 50,000 and it
is likely that the nature of a graph with 100M edges is not
affected.
In the first experiment, about detecting bipartite
communities, we introduce 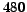 dense bipartite subgraphs. More precisely we
introduce
dense bipartite subgraphs. More precisely we
introduce 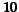 bipartite
subgraphs for each of the
bipartite
subgraphs for each of the 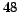 categories representing all possible combinations
of number of fans, number of centers, and density over a number
of fans is chosen in
categories representing all possible combinations
of number of fans, number of centers, and density over a number
of fans is chosen in
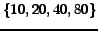 ; number of centers chosen in
; number of centers chosen in
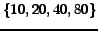 ; and density randomly chosen in
the ranges
; and density randomly chosen in
the ranges ![$[0.25,0.5]$](www015-pellegrini-img158.png) (low),
(low), ![$[0.5,0.75]$](www015-pellegrini-img159.png) (medium), and
(medium), and ![$[0.75,1]$](www015-pellegrini-img160.png) (high).
(high).
Moreover, the fans and centers of every new community are
chosen so that they don't intersect any community found in the
original graph nor any other new community. The following table
(Table 1) shows how many added
communities are found in average over 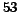 experiments.
For every one of the
experiments.
For every one of the 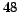 types, the maximum recall number is
types, the maximum recall number is 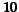 .
.
Table 1: Number of added bipartite
communities found with threshold=8 depending on
number of fans, centers, and density.
| # Centers |
80 |
0 |
5.2 |
9.6 |
10 |
|
1.2 |
8.4 |
9.7 |
10 |
|
5.7 |
8.6 |
9.5 |
9.8 |
| 40 |
0 |
5.4 |
9.5 |
9.9 |
0.7 |
8 |
9.7 |
9.9 |
5.4 |
8.6 |
9.7 |
9.8 |
| 20 |
0 |
2.7 |
5.4 |
6 |
0.9 |
7.9 |
9.6 |
9.9 |
4.6 |
8.4 |
9.6 |
9.9 |
| 10 |
0 |
0 |
0 |
0 |
0.1 |
0.8 |
1.9 |
3.2 |
3.3 |
6.5 |
9 |
9.7 |
| |
10 |
20 |
40 |
80 |
10 |
20 |
40 |
80 |
10 |
20 |
40 |
80 |
| # of Fans |
# of Fans |
# of Fans |
| Low density |
Med. density |
High density |
In the second experiment, about detecting cliques , we
introduce ten cliques for each of 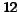 classes representing all possible combinations
over: number of pages in
classes representing all possible combinations
over: number of pages in
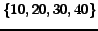 , and density randomly chosen in
the ranges
, and density randomly chosen in
the ranges ![$[0.25,0.5]$](www015-pellegrini-img158.png) ,
, ![$[0.5,0.75]$](www015-pellegrini-img159.png) , and
, and ![$[0.75,1]$](www015-pellegrini-img160.png) . The following table (Table 2) shows how many such cliques are
found in average over
. The following table (Table 2) shows how many such cliques are
found in average over 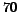 experiments. Again the maximum recall number per
entry is 10.
experiments. Again the maximum recall number per
entry is 10.
Table 2: Number of added clique
communities found with threshold=8 depending on
number of pages and density.
| # pages |
40 |
9.6 |
9.8 |
9.7 |
| 30 |
8.5 |
9.4 |
9.3 |
| 20 |
3.6 |
7.6 |
8.3 |
| 10 |
0 |
0.1 |
3.5 |
| |
Low |
Med |
High |
| Density |
The cleaned .it 2004 graph used for the test has an average
degree roughly 6 (see Section 6). A small bipartite graph of
10-by-10 nodes or a small clique of 10 nodes at 50% density has
an average degree of 5. The breakdown of the degree-counting
heuristic for these low thresholds is easily explained with the
fact that these small and sparse communities are effectively
hard to distinguish from the background graph by simple degree
counting.
6 Large communities in the Web
In this section we apply our algorithm to the task of
extracting and classifying real large communities in the
web.
For our experiments we have used data from The Stanford
WebBase project [11]
and data from the WebGraph project [5,4]. Raw data is
publicly available at http://law.dsi.unimi.it/. More
precisely we apply our algorithm on three graphs: the graph
that represents a snapshot of the Web of the year 2001 (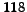 M pages and
M pages and
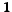 G links); the
graph that represents a snapshot of the Italian domain of the
year 2004 (
G links); the
graph that represents a snapshot of the Italian domain of the
year 2004 (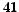 M
pages and
M
pages and 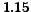 G arcs); the
graph that represents a snapshot of the United Kingdom domain
of the year 2005 (
G arcs); the
graph that represents a snapshot of the United Kingdom domain
of the year 2005 (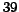 M
pages and
M
pages and 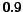 G links).
G links).
Since we are searching communities by the study of social
links, we first remove all nepotistic links, i.e., links
between two pages that belong to the same domain (this is a
standard cleaning step used also in [31]). Once these links
are removed, we remove also all isolated pages, i.e.,
pages with both outdegree and indegree equal to zero. Observe
that we don't remove anything else from the graph, for example
we don't need to remove small outdegree pages and large
indegree pages, as it is usually done for efficiency reasons,
since our algorithm handles these cases efficiently and
correctly. We obtain the reduced data sets shows in Table 3.
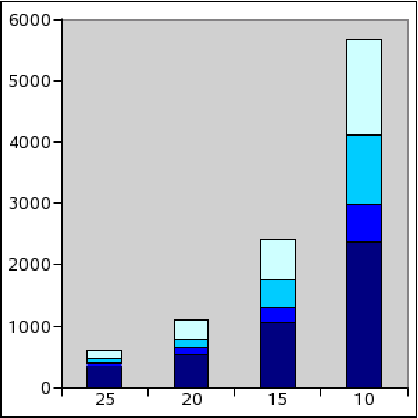
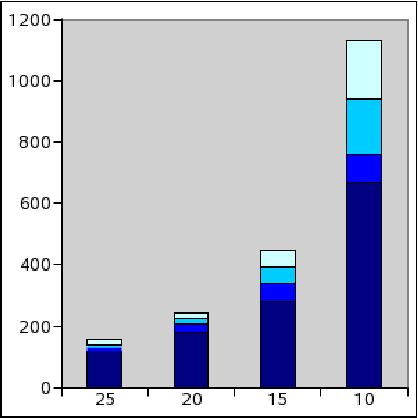
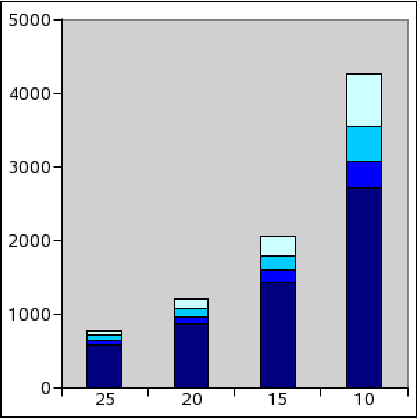
Figure 5 presents the results
obtained with the three graphs presented before. The  axe shows how
many communities are found, and the
axe shows how
many communities are found, and the 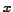 axe represents the value of the parameter
axe represents the value of the parameter
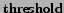 . Moreover communities are
partitioned by density into four categories (shown in
grey-scale) corresponding to density intervals: [1,0.75],
. Moreover communities are
partitioned by density into four categories (shown in
grey-scale) corresponding to density intervals: [1,0.75], ![$]0.75,~0.5]$](www015-pellegrini-img179.png) ,
, ![$]0.5,~0.25]$](www015-pellegrini-img180.png) ,
, ![$]0.25,0.00]$](www015-pellegrini-img181.png) .
.
Table 4 reports the time needed
for the experiments with an Intel Pentium IV 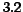 Ghz single
processor computer using 3.5 GB RAM memory. The data sets,
although large, were in a cleverly compressed format and could
be stored in main memory. The column ``# loops'' shows the
average number of iterative refinement done for each community
in Algorithm
Ghz single
processor computer using 3.5 GB RAM memory. The data sets,
although large, were in a cleverly compressed format and could
be stored in main memory. The column ``# loops'' shows the
average number of iterative refinement done for each community
in Algorithm
 . Depending on the fan out
degree threshold, time ranges from a few minutes to just above
two hours for the most intensive computation. Table 5 shows the effectiveness of the
degree-based filter since in the large tests just only
. Depending on the fan out
degree threshold, time ranges from a few minutes to just above
two hours for the most intensive computation. Table 5 shows the effectiveness of the
degree-based filter since in the large tests just only 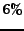 to
to 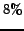 of the
invocations to
of the
invocations to
 do not return a community.
Note that this false-positive rate of the first stage does not
impact much on the algorithm's efficiency nor on the
effectiveness. The false positives of the first stage are
caught anyhow by the second stage.
do not return a community.
Note that this false-positive rate of the first stage does not
impact much on the algorithm's efficiency nor on the
effectiveness. The false positives of the first stage are
caught anyhow by the second stage.
Interestingly in Table 7 it
is shown the coverage of the communities with respect to the
nodes of sufficiently high degree. In two national domains the
percentage of nodes covered by a community is above 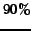 for national
domains, and just below
for national
domains, and just below  for the web graph (of 2001). Table 6 shows the distribution of size
and density of communities found. The web 2001 data set seems
richer in communities with few fans (range [10-25]) and poorer
in communities with many fans (range
for the web graph (of 2001). Table 6 shows the distribution of size
and density of communities found. The web 2001 data set seems
richer in communities with few fans (range [10-25]) and poorer
in communities with many fans (range 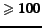 )
and this might explain the lower coverage.
)
and this might explain the lower coverage.
Table 4: Measurements of performance.
Number of communities found, total computing time and
average number of cleaning loops per community.
| |
Web 2001 |
|
Italy 2004 |
|
Uk 2005 |
| Thresh. |
# com. |
# loops |
Time |
# com. |
# loops |
Time |
# com. |
# loops |
Time |
| 10 |
5686 |
2.7 |
2h12min |
1099 |
2.7 |
30min |
4220 |
2.5 |
1h10min |
| 15 |
2412 |
2.8 |
1h03min |
452 |
2.8 |
17min |
2024 |
2.6 |
38min |
| 20 |
1103 |
2.8 |
31min |
248 |
2.8 |
10min |
1204 |
2.7 |
27min |
| 25 |
616 |
2.6 |
19min |
153 |
2.8 |
7min |
767 |
2.7 |
20 min |
Table 5: Number and percentage of useless
calls to
 .
.
| |
Web 2001 |
Italy 2004 |
Uk 2005 |
| Thresh. |
Num. |
perc. |
Num. |
perc. |
Num. |
perc. |
| 10 |
364 |
6% |
34 |
3% |
377 |
8% |
| 15 |
135 |
5% |
24 |
5% |
331 |
14% |
| 20 |
246 |
18% |
24 |
9% |
526 |
30% |
| 25 |
148 |
19% |
4 |
3% |
323 |
30% |
Table 6 shows how many
communities are found with the
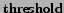 equal to
equal to 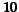 , in the three
data sets in function of number of fans, centers, and density.
Low, medium and high densities are respectively the ranges
, in the three
data sets in function of number of fans, centers, and density.
Low, medium and high densities are respectively the ranges ![$[0.25,0.5]$](www015-pellegrini-img158.png) ,
, ![$[0.5,0.75]$](www015-pellegrini-img159.png) , and
, and
![$[0.75,1]$](www015-pellegrini-img160.png) .
.
Table 6: Distribution of the detected
communities depending on number of fans, centers, and
density, for 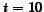 .
.
|
Web 2001 - 5686 communities found at t=10
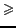 100 100 |
92 |
21 |
49 |
24 |
5 |
8 |
7 |
2 |
8 |
6 |
1 |
11 |
| [50, 100[ |
185 |
35 |
48 |
38 |
11 |
26 |
9 |
7 |
16 |
11 |
9 |
22 |
| [25, 50[ |
247 |
54 |
136 |
52 |
28 |
89 |
17 |
6 |
52 |
13 |
14 |
100 |
| [10, 25[ |
167 |
68 |
437 |
13 |
29 |
217 |
1 |
20 |
163 |
17 |
23 |
347 |
| |
low |
med |
high |
low |
med |
high |
low |
med |
high |
low |
med |
high |
| Density |
Density |
Density |
Density |
| [10,
25[ |
[25,
50[ |
[50,
100[ |
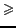 100 100 |
| # of
Fans |
|
|
Italy 2004 - 1999 communities found at t=10
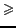 100 100 |
17 |
3 |
11 |
3 |
1 |
5 |
2 |
2 |
0 |
2 |
1 |
12 |
| [50, 100[ |
32 |
2 |
14 |
14 |
2 |
4 |
5 |
1 |
2 |
3 |
4 |
15 |
| [25, 50[ |
28 |
15 |
33 |
10 |
2 |
18 |
5 |
7 |
16 |
19 |
11 |
69 |
| [10, 25[ |
14 |
5 |
42 |
1 |
3 |
26 |
1 |
2 |
34 |
5 |
11 |
247 |
| |
low |
med |
high |
low |
med |
high |
low |
med |
high |
low |
med |
high |
| Density |
Density |
Density |
Density |
| [10,
25[ |
[25,
50[ |
[50,
100[ |
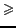 100 100 |
| # of Fans |
|
|
United Kingdom 2005 - 4220 communities found at t=10
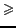 100 100 |
24 |
5 |
18 |
17 |
4 |
15 |
10 |
3 |
14 |
11 |
5 |
51 |
| [50, 100[ |
63 |
23 |
55 |
14 |
21 |
34 |
19 |
11 |
42 |
24 |
22 |
81 |
| [25, 50[ |
76 |
23 |
151 |
28 |
18 |
159 |
16 |
7 |
68 |
51 |
22 |
273 |
| [10, 25[ |
43 |
30 |
299 |
7 |
8 |
266 |
8 |
11 |
159 |
34 |
44 |
705 |
| |
low |
med |
high |
low |
med |
high |
low |
med |
high |
low |
med |
high |
| Density |
Density |
Density |
Density |
| [10,
25[ |
[25,
50[ |
[50,
100[ |
 100 100 |
| # of Fans |
|
Table 7: Coverage of communities found in
the web graphs. The leftmost column shows the threshold
value. For each data set, the first column is the number
of pages with
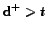 , and the second and third
columns are the number and percentage of pages that have
been found to be a fan of some community.
, and the second and third
columns are the number and percentage of pages that have
been found to be a fan of some community.
| |
Web 2001 |
Italy 2004 |
Uk 2005 |
| Thresh. |
# Total |
# in Com. |
Perc. |
# Total |
# in Com. |
Perc. |
# Total |
# in Com. |
Perc. |
| 10 |
984290 |
581828 |
59% |
3331358 |
3031723 |
91% |
4085309 |
3744159 |
92% |
| 15 |
550206 |
286629 |
52% |
2225414 |
2009107 |
90% |
3476321 |
3172338 |
91% |
| 20 |
354971 |
164501 |
46% |
1761160 |
642960 |
37% |
2923794 |
2752726 |
94% |
| 25 |
244751 |
105500 |
43% |
487866 |
284218 |
58% |
2652204 |
2503226 |
94% |
7 Visualization of communities
The compressed data structure in [5] storing the web graph
does not hold any information about the textual content of the
pages. Therefore, once the list of url's of fans and centers
for each community has been created, a non-recursive crawl of
the WWW focussed on this list of url's has been performed in
order to recover textual data from communities.
What we want is to obtain an approximate description of the
community topics. The intuition is that the topic of a
community is well described by its centers. As good summary of
the content of a center page we extract the text contained in
the title tag of the page. We treat fan pages in a different
way. The full content of the page is probably not interesting
because a fan page can contain different topics, or might even
be part of different communities. We extract only the anchor
text of the link to a center page because it is a good textual
description of the edge from the fan to a center in the
community graph. For each community we build a weighted set of
words getting all extracted words from centers and fans. The
weight of each word takes into account if a word cames from a
center and/or a fan and if it is repeated. All the words in a
stop word list are removed. We build a flat clustering of the
communities. For clustering we use the k-center algorithm
described in [18,17]. As a
metric we adopt the Generalized Jaccard distance (a weighted
form of the standard Jaccard distance).
This paper focusses on the algorithmic principles and
testing of a fast and effective heuristic for detecting
large-to-medium size dense subgraphs in the web graph. The
examples of clusters reported in this section are to be
considered as anecdotical evidence of the capabilities of the
Community Watch System. We plan on using the Community Watch
tool for a full-scale analysis of portions of the Web Graph as
future research. In Table 8
we show some high quality clusters of community found by the
Community Watch tool in the data-set UK2005 among those
communities detected with threshold 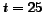 (767 communities). Further filtering of
communities with too few centers reduces the number of items
(communities) to 636. The full listing can be inspected by
using the Community Watch web interface publicly
available at http://comwatch.iit.cnr.it.
(767 communities). Further filtering of
communities with too few centers reduces the number of items
(communities) to 636. The full listing can be inspected by
using the Community Watch web interface publicly
available at http://comwatch.iit.cnr.it.
Table 8: Some notable clusters of
communities in the data set UK05 for 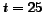 .
Parameters used for filtering and clustering: #
fans=0-1000, # centers=10-max, average degree =10-max,
taget=70 clusters (55 done). Communities in the filtered
data set: 636. We report, for each cluster, id number,
keywords with weights, number of communities in the
cluster and how many of these are relevant to the
prevalent type.
.
Parameters used for filtering and clustering: #
fans=0-1000, # centers=10-max, average degree =10-max,
taget=70 clusters (55 done). Communities in the filtered
data set: 636. We report, for each cluster, id number,
keywords with weights, number of communities in the
cluster and how many of these are relevant to the
prevalent type.
| Cl. ID |
Cl. Keywords |
# Comm. |
# Rel. Comm. |
Prevalent Type |
| 1 |
poker (0.66) casino (1.0) games
(0.80) |
(8) |
8 |
- gambling |
| 2 |
phone (0.71) nokia (1.0)
motorola (0.31) |
(17) |
17 |
- mobile phones |
| 10 |
men (0.15) lingerie (0.16) women
(0.23) |
(14) |
14 |
- clothing/underware |
| 14 |
antique (1.0) auction (0.11)
search (0.19) |
(5) |
4 |
- antiques |
| 22 |
car (1.0) hire (0.29) cheap
(0.13) |
(25) |
20 |
- car sales/rent |
| 25 |
hotel (0.65) holiday (1.0)
travel (0.22) |
(36) |
34 |
- turism/travel |
| 27 |
delivery (0.31) flowers (1.0)
gifts (0.66) |
(8) |
8 |
- gifts and flowers |
| 31 |
credit (0.54) loans (1.0)
insurance (0.56) |
(36) |
28 |
- financial services |
| 32 |
city (0.59) council (1.0)
community (0.31) |
(7) |
6 |
- city councils |
In this paper we tackle the problem of finding dense
sub-graphs of the web-graph. We propose an efficient heuristic
method that is shown experimentally to be able to discover
about  of
communities having about 20 fans/centers, even at medium
density (above
of
communities having about 20 fans/centers, even at medium
density (above  ).
The effectiveness increases and approaches
).
The effectiveness increases and approaches 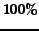 for larger
and denser communities. For communities of less than 20
fans/centers (say 10 fans and 10 centers) our algorithm is
still able to detect a sizable fraction of the communities
present (about
for larger
and denser communities. For communities of less than 20
fans/centers (say 10 fans and 10 centers) our algorithm is
still able to detect a sizable fraction of the communities
present (about 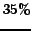 )
whenever these are at least
)
whenever these are at least 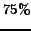 dense. Our method is effective for a medium
range of community size/density which is not well detected by
the current technology. One can cover the whole spectrum of
communities by applying first our method to detect large and
medium size communities, then, on the residual graph, the
Trawling algorithm to find the smaller communities left. The
efficiency of the Trawling algorithm is likely to be boosted by
its application to a residual graph purified of larger
communities that tend to be re-discovered several times. We
plan the coupling of our heuristic with the Trawling algorithm
as future work. One open problem is that of devising an
efficient version the
dense. Our method is effective for a medium
range of community size/density which is not well detected by
the current technology. One can cover the whole spectrum of
communities by applying first our method to detect large and
medium size communities, then, on the residual graph, the
Trawling algorithm to find the smaller communities left. The
efficiency of the Trawling algorithm is likely to be boosted by
its application to a residual graph purified of larger
communities that tend to be re-discovered several times. We
plan the coupling of our heuristic with the Trawling algorithm
as future work. One open problem is that of devising an
efficient version the
 in the data stream model
in order to cope with instances of the web-graph stored in
secondary memory. This feature is important when a limited
amount of core memory is available.
in the data stream model
in order to cope with instances of the web-graph stored in
secondary memory. This feature is important when a limited
amount of core memory is available.
REFERENCES
[1]
J. Abello, M. G. C. Resende, and S. Sudarsky.
Massive quasi-clique detection.
In Latin American Theoretical Informatics (LATIN), pages 598-612, 2002.
[2]
K. Bharat, A. Z. Broder, J. Dean, and M. R. Henzinger.
A comparison of techniques to find mirrored hosts on the WWW.
Journal of the American Society of Information Science, 51(12):1114-1122, 2000.
[3]
M. Bianchini, M. Gori, and F. Scarselli.
Inside pagerank.
ACM Trans. Inter. Tech., 5(1):92-128, 2005.
[4]
P. Boldi, B. Codenotti, M. Santini, and S. Vigna.
Ubicrawler: A scalable fully distributed web crawler.
Software: Practice and Experience, 34(8):711-726, 2004.
[5]
P. Boldi and S. Vigna.
The webgraph framework I: Compression techniques.
In WWW '04, pages 595-601, 2004.
[6]
A. Broder, R. Kumar, F. Maghoul, P. Raghavan, S. Rajagopalan, R. Stata, A. Tomkins, and J. Wiener.
Graph structure in the web.
Computer Networks, 33(1-6):309-320, 2000.
[7]
A. Z. Broder, M. Charikar, A. M. Frieze, and M. Mitzenmacher.
Min-wise independent permutations.
Journal of Computer and System Sciences, 60(3):630-659, 2000.
[8]
A. Z. Broder, S. C. Glassman, M. S. Manasse, and G. Zweig.
Syntactic clustering of the web.
In Selected papers from the sixth international conference on World Wide Web, pages 1157-1166, Essex, UK, 1997. Elsevier Science Publishers Ltd.
[9]
A. Capocci, V. D. P. Servedio, G. Caldarelli, and F. Colaiori.
Communities detection in large networks.
In WAW 2004: Algorithms and Models for the Web-Graph: Third International Workshop, pages 181-188, 2004.
[10]
S. Chakrabarti, B. E. Dom, S. R. Kumar, P. Raghavan, S. Rajagopalan, A. Tomkins, D. Gibson, and J. Kleinberg.
Mining the link structure of the world wide web.
Computer, 32(8):60-67, 1999.
[11]
J. Cho and H. Garcia-Molina.
WebBase and the stanford interlib project.
In 2000 Kyoto International Conference on Digital Libraries: Research and Practice, 2000.
[12]
U. Feige.
Relations between average case complexity and approximation complexity.
In Proc. of STOC 2002, Montreal., 2002.
[13]
U. Feige and M. Langberg.
Approximation algorithms for maximization problems arising in graph partitioning.
Journal of Algorithms, 41:174-211, 2001.
[14]
U. Feige, D. Peleg, and G. Kortsarz.
The dense $k$-subgraph problem.
Algorithmica, 29(3):410-421, 2001.
[15]
G. W. Flake, S. Lawrence, and C. L. Giles.
Efficient identification of web communities.
In KDD '00, pages 150-160, New York, NY, USA, 2000. ACM Press.
[16]
G. W. Flake, S. Lawrence, C. L. Giles, and F. Coetzee.
Self-organization of the web and identification of communities.
IEEE Computer, 35(3):66-71, 2002.
[17]
F. Geraci, M. Maggini, M. Pellegrini, and F. Sebastiani.
Cluster generation and cluster labelling for web snippets.
In (SPIRE 2006), pages 25-36, Glasgow, UK., October 2006.
Volume 4209 in LNCS.
[18]
F. Geraci, M. Pellegrini, P. Pisati, and F. Sebastiani.
A scalable algorithm for high-quality clustering of web snippets.
In In Proceedings of the 21st Annual ACM Symposium on Applied Computing (SAC 2006), pages 1058-1062, Dijon, France, April 2006.
[19]
D. Gibson, J. Kleinberg, and P. Raghavan.
Inferring web communities from link topology.
In HYPERTEXT '98, pages 225-234, New York, NY, USA, 1998. ACM Press.
[20]
D. Gibson, R. Kumar, and A. Tomkins.
Discovering large dense subgraphs in massive graphs.
In VLDB '05, pages 721-732. VLDB Endowment, 2005.
[21]
M. Girvan and M. E. J. Newman.
Community structure in social and biological networks.
Proc. Natl. Acad. Sci. USA, pages 7821-7826, 2002.
[22]
A. Gulli and A. Signorini.
The indexable web is more than 11.5 billion pages.
In WWW (Special interest tracks and posters), pages 902-903, 2005.
[23]
Z. Gyöngyi and H. Garcia-Molina.
Web spam taxonomy.
In First International Workshop on Adversarial Information Retrieval on the Web, 2005.
[24]
Q. Han, Y. Ye, H. Zhang and J. Zhang.
Approximation of dense 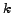 -subgraph, 2000.
Manuscript.
-subgraph, 2000.
Manuscript.
[25]
J. Hastad.
Clique is hard to approximate within
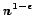 Acta Mathematica, 182:105-142, 1999.
Acta Mathematica, 182:105-142, 1999.
[26]
M. Henzinger.
Algorithmic challenges in web search engines.
Internet Mathematics, 1(1):115-126, 2002.
[27]
N. Imafuji and M. Kitsuregawa.
Finding a web community by maximum flow algorithm with hits score based capacity.
In DASFAA 2003, pages 101-106, 2003.
[28]
H. Ino, M. Kudo, and A. Nakamura.
Partitioning of web graphs by community topology.
In WWW '05, pages 661-669, New York, NY, USA, 2005. ACM Press.
[29]
H. Kautz, B. Selman, and M. Shah.
Referral Web: Combining social networks and collaborative filtering.
Communications of the ACM, 40(3):63-65, 1997.
[30]
R. Kumar, P. Raghavan, S. Rajagopalan, and A. Tomkins.
Extracting large-scale knowledge bases from the web.
In VLDB '99, pages 639-650, San Francisco, CA, USA, 1999. Morgan Kaufmann Publishers Inc.
[31]
R. Kumar, P. Raghavan, S. Rajagopalan, and A. Tomkins.
Trawling the Web for emerging cyber-communities.
Computer Networks (Amsterdam, Netherlands: 1999), 31(11-16):1481-1493, 1999.
[32]
R. Kumar, P. Raghavan, S. Rajagopalan, and A. Tomkins.
Method and system for trawling the world-wide web to identify implicitly-defined communities of web pages.
US patent 6886129, 2005.
[34]
R. Lempel and S. Moran.
The stochastic approach for link-structure analysis (SALSA) and the TKC effect.
Computer Networks (Amsterdam, Netherlands: 1999), 33(1-6):387-401, 2000.
[35]
M. Newman.
The structure and function of complex networks.
SIAM Review, 45(2):167-256, 2003.
[36]
P. K. Reddy and M. Kitsuregawa.
An approach to relate the web communities through bipartite graphs.
In WISE 2001, pages 301-310, 2001.
[37]
B. Wu and B. D. Davison.
Identifying link farm spam pages.
In WWW '05, pages 820-829, New York, NY, USA, 2005. ACM Press.
Footnotes
- 1
- It is sufficient to eliminate nodes of
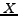 of outdegree
smaller than
of outdegree
smaller than 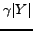 , and from
, and from 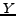 those of
indegree smaller than
those of
indegree smaller than 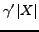 .
.
- 2
- S. Vigna and P. Boldi, personal communication.
![]() of the arcs present. At the lower extremes the algorithm
catches 35% of dense communities made of ten nodes. We
complete our Community Watch system by clustering
the communities found in the web-graph into homogeneous
groups by topic and labelling each group by representative
keywords.
of the arcs present. At the lower extremes the algorithm
catches 35% of dense communities made of ten nodes. We
complete our Community Watch system by clustering
the communities found in the web-graph into homogeneous
groups by topic and labelling each group by representative
keywords.
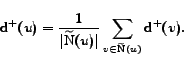
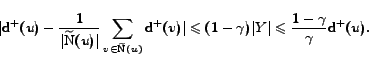
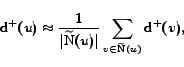

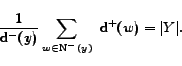
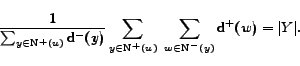
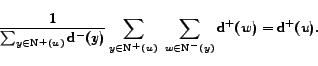
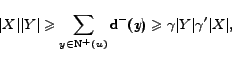
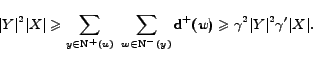
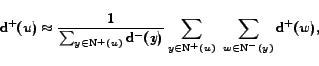
![\begin{figure} \begin{center} \subfigure[Communities sharing fans]{\scalebox{... ...ox{.5}{% \input{IntersectCommunities2.pstex_t}}} \end{center} \end{figure}](www015-pellegrini-img150.png)